Task
Little Tree is interested in trees of various sizes. She has a rooted binary tree (i.e.~one where every vertex has at most 2 children), not necessarily a balanced tree, in front of her, whose root is denoted by and whose vertices are labeled . The label of any vertex is always strictly less than any of its children.
A set of vertices is called valid if no vertex in is the ancestor of any other vertex in . The value of , denoted by , is given by the number of vertices within the tree that have any vertex of as an ancestor. (We consider a node to be its own ancestor.) In other words, it is the sum of the sizes of the subtrees rooted at vertices in .
Her enemy, Little Cactus, challenges her to the following task: Given and the tree , create as many valid, nonempty sets as possible, such that
and for any .
Input data
The first line of the input file contains the integer . The second line contains integers , separated by spaces, where denotes the parent of node .
Output data
Output , the number of sets you can create, followed by each of the sets on its own line. To output a set, first output its size, then its elements, separated by spaces.
Constraints and clarifications
- .
- If you output an incorrect solution (i.e.~one using too many vertices, or where two sets have the same value) then you will receive 0 points for a test. Otherwise, the fraction of the score you will receive for a particular test will be equal to .
| # | Points | Clarifications |
|---|---|---|
| 1 | 7 | for |
| 2 | 12 | |
| 3 | 13 | |
| 4 | 21 | |
| 5 | 26 | |
| 6 | 21 | No further restrictions |
Example 1
stdin
2
1 2 3
stdout
4
1 4
1 3
1 2
1 1
Explanation
The tree is given by
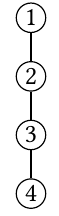
We see that the sets , , , all have distinct values (namely 1, 2, 3, 4 respectively), and have total size . Hence this output is correct.
Example 2
stdin
2
1 2 2
stdout
4
1 4
2 3 4
1 2
1 1
Explanation
The tree is given by
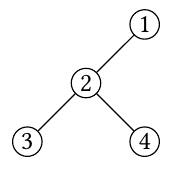
We see that the sets , , , all have distinct values (namely 1, 2, 3, 4 respectively), and have total size . Hence this output is correct.