Grow Gravity

Task

Little Newton likes gravity and plays with a magical shape made out of $1 \times 1$ squares, suspended in the air.

Initially, this shape is made of only one such square. On this magical shape two things happen (in this order):

1. Grow phase: Around each square in this shape some new squares will appear. The grow phase can be of two types:
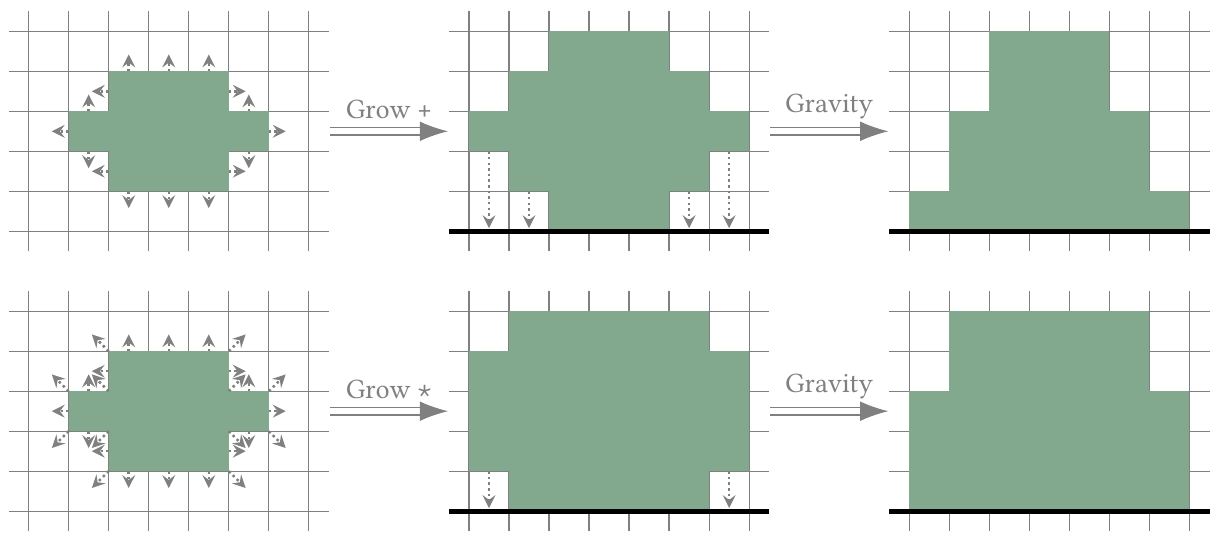
   • Type + The new squares will appear around the squares in only 4 directions (north, south, east and west).
   • Type * The new squares will appear in 8 directions (north, south, east, west, north-east, north-west, south-east and south-west).
2. Gravity phase: In this phase, Little Newton places a plate under the shape and lets all the squares fall onto it. Note: The plate is removed immediately after this operation!

As an example, the effects of each of the 2 types of grow phases, followed by a gravity phase, are pictured below.

Little Newton has an array $v_1, \ldots, v_N$ of $N$ types of grow phases and wants to do $Q$ operations of the following types:

• $\text{update}(i)$: If $v_i = +$ then set it to $*$; otherwise if $v_i = *$ set it to $+$.
• $\text{query}(\ell, r)$: Suppose Little Newton starts with a shape made out of only one $1 \times 1$ square and applies, for $i = \ell, \ldots, r$, in order, a grow phase of type $v_i$ followed by a gravity phase. How many $1 \times 1$ squares will the shape have in the end?

Help Little Newton answer all of these queries.

Input data

The first line of the input contains the number $N$. The second line contains $N$ symbols from among $\{ +, *\}$, not separated by spaces, representing the initial values of $v_1, \ldots, v_N$. The third line of the input contains the number $Q$. Then, each of the following $Q$ lines will contain one of the following: either two integers $1\, i$ representing an $\text{update}(i)$ operation, or three integers $2\,\ell\,r$ representing a $\text{query}(\ell, r)$ operation.

Output data

You should output the answer for each $\text{query}(\ell, r)$ operation, each on a new line.

Constraints and clarifications

• $1 \leq N \leq 200 \ 000$.
• $1 \leq Q \leq 200 \ 000$.
• $v_i \in \{ +, * \}$ for $1 \leq i \leq N$.
• $t \in \{ 1, 2\}$, $1 \leq i \leq N$ and $1 \leq \ell \leq r \leq N$ for each operation.

Example

stdin

4
+*++
9
2 2 4
1 3
1 4
2 2 4
1 1
1 2
1 3
1 4
2 2 4

stdout

39
49
31

Explanation

First query. In this query, the sequence of operations is *++. The shape thus has the following configurations.

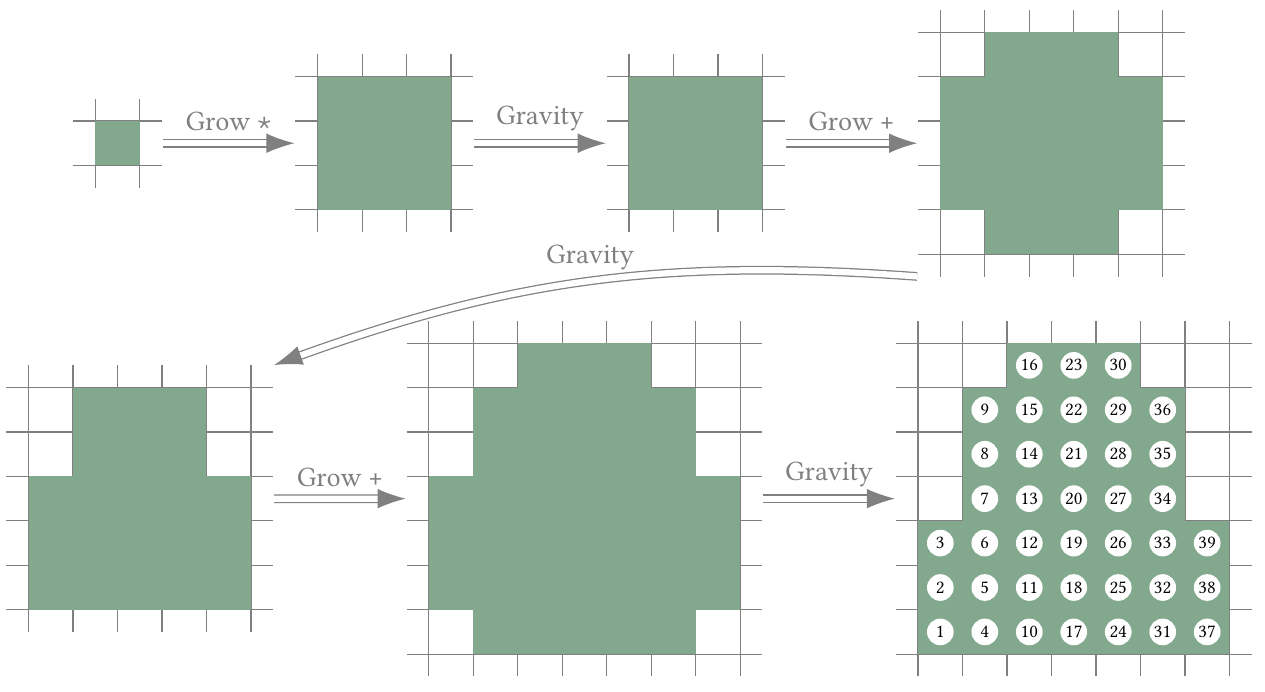
Hence the answer is $39$.

Second query. In the second query, the sequence of operations is ***. The shape thus has the following configurations.

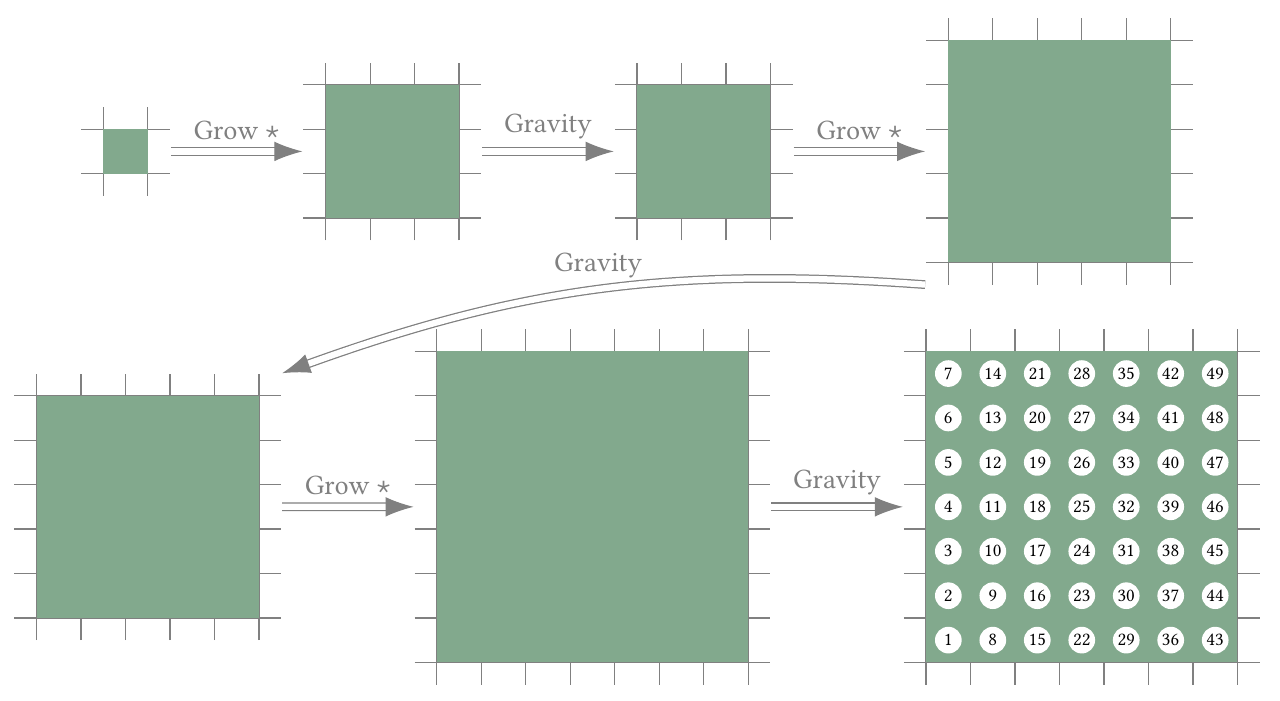
Therefore, the answer is $49$.

Third query. In the last query, the sequence of operations is +++. The shape thus has the following configurations.

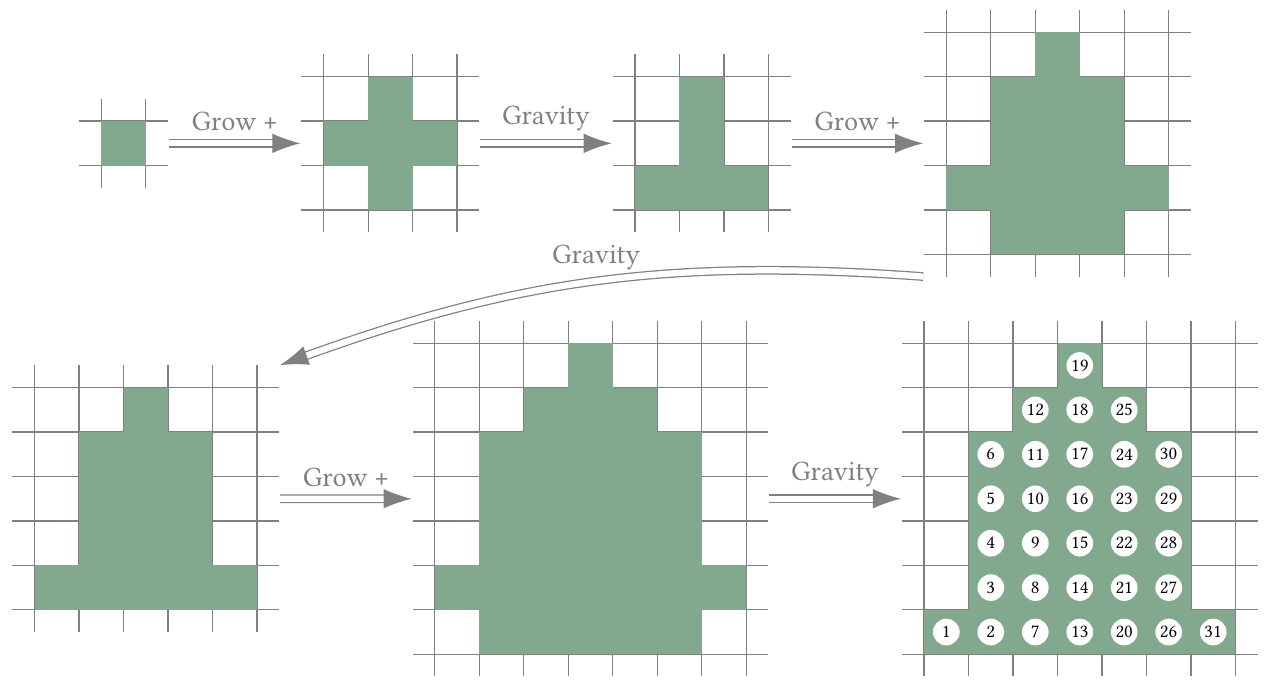
Thus, the answer is $31$.