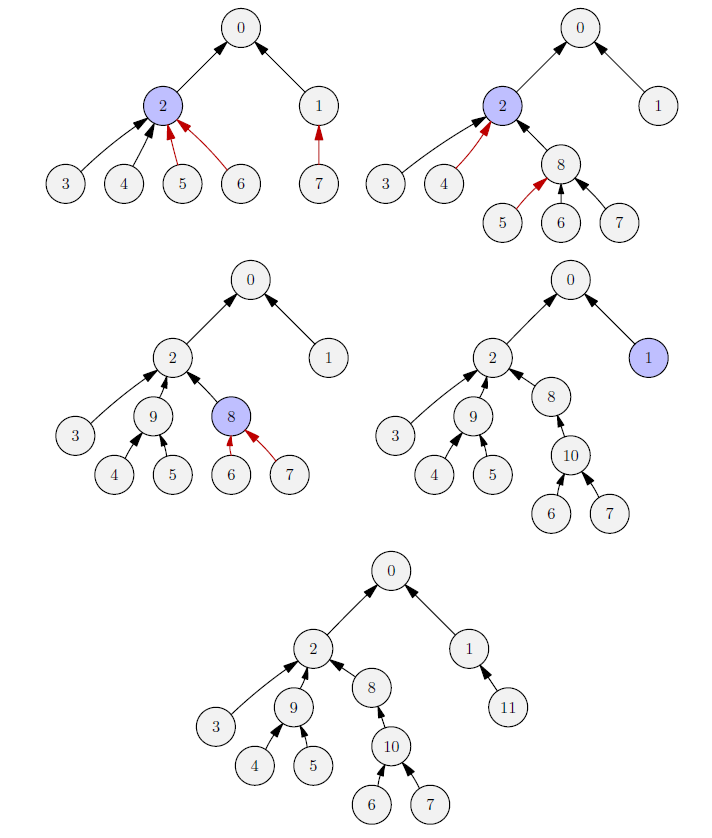
William has finally solved the nasty “L/10-L/16-bipasso” problem, and is now ready to start earning money immediately! For this noble purpose, he arranged his fully functional computers (numbered from to ) into a tree-shaped network rooted at server , so that computer is a “slave” of computer (conventionally, we assume that ). Now the most demanding tasks from all over the world are being delivered to his farm, and will eventually be completed (hopefully)!
Sadly, some of his computers are already experiencing severe heating problems, not being able to handle the output of all of their slaves. Since the recycling bin for electronic waste is always filling up, William can promptly solve this emergencies through proxying: when some computers are overheating, William selects of their slaves , , and delegates those to a newly-recycled proxy. Afterwards, the proxy is connected to another computer .
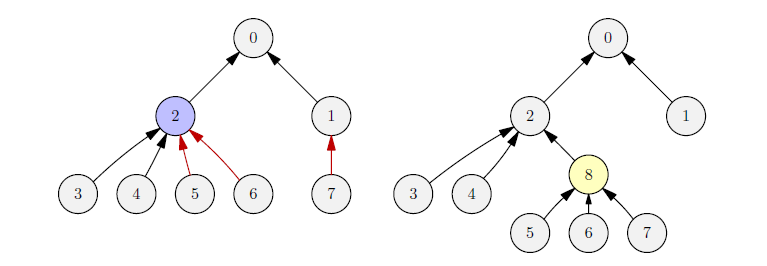
In this case, computers and are overheating (left) thus William delegates of their slaves (computers , , and ) to the new proxy , connecting it to computer . Even though this reconfiguration can solve the overheating problem, William is worried that the tree structure would grow too high, slowing down the computations. What is worse, a wrong reconfiguration could even create a cycle causing an infinite data flow!
Given a sequence of reconfigurations, help William keep track of the situation by determining whether each emergency causes the height to increase or, even worse, creates a cycle.
Input data
The first line contains integers , . The second line contains integers , , , . Each of the following lines contains integers , followed on the same line by integers , , , .
Output data
You need to write a single line with a sequence of characters, such that the -th character is:
c: if the -th reconfiguration creates a cycle;1: if the -th reconfiguration causes the tree height to increase;0: if the -th reconfiguration does not cause the tree height to increase.
You need to output a character until either a cycle is created or the reconfigurations are finished. In other words, the sequence can either consist of characters among and or less than characters among and followed by a single c.
Constraints and clarifications
- .
- .
- for each , .
- in each emergency.
- The master/slave structure forms a tree (there are no circular links).
- The height of the tree never grows above .
| # | Score | Constraints |
|---|---|---|
| 1 | 5 | Examples |
| 2 | 25 | |
| 3 | 30 | |
| 4 | 20 | ’s master is , for each and reconfiguration. |
| 5 | 20 | No additional limitations. |
Example 1
stdin
3 5
-1 0 0
0 2 1 2
3 0
2 2 4 3
1 1 0
6 5 4 2 3 1 5
stdout
10c
Explanation
In the first sample case, the network structure evolves as follows:
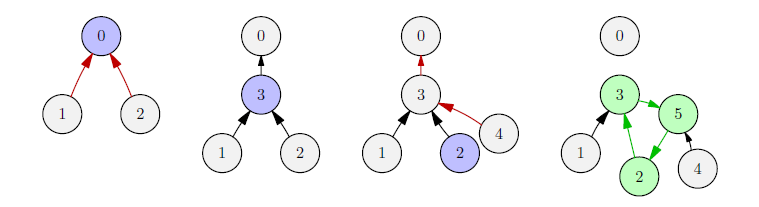
After the third reconfiguration, a cycle is detected hence the following reconfigurations do not take place.
Example 2
stdin
8 4
-1 0 0 2 2 2 2 1
2 3 5 6 7
2 2 5 4
8 2 6 7
1 0
stdout
1010
Explanation
The second sample case corresponds to the structure described in the text, which evolves as follows: