
William is playing a city simulation game: the main objective is to save the mayor’s life in the event of natural disasters and the weather forecast just warned William about an imminent flooding!
The city can be seen as a straight line: there are positions numbered from to . The mayor’s house is in position . During the flooding, liters of water will flow from the left corner to position first, then to position and so on. In order to stop the water from flooding the mayor’s home, you need to place manholes in every position except the one in which the house of the mayor is located. Luckily, you have exactly manholes left in the game inventory, however, they are all different. Some are able to “subtract” more water than others: no two manholes will subtract the same amount!
For example, let’s say that liters of water will rain down during the flooding. Moreover, let’s assume that the city has total positions (numbered from to ), and that is the position of the mayor’s house. In this case, we would have manholes in our inventory. Let’s say that the manholes are able to remove, respectively: , , and liters of water.
In this case, we can see that there are only ways to arrange the manholes so that some water will hit the mayor’s home (indicated with a ). To be precise, - () = liters of water will reach his home.
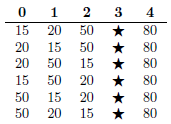
So, the number of bad manhole arrangements is . Since the total number of arrangements is , we can deduce that the answer for this case is .
Compute how many ways William can put the manholes in such a way that will keep the mayor’s house dry during the flooding.
Input data
The first line contains a single integer: . The second line contains two integers: and . The third line contains integers : the “capacity” of the manholes.
Output data
You need to write a single line with an integer: the number of good manhole arrangements. Since this number can be huge, just print the remainder when dividing it by .
Constraints and clarifications
- .
- .
- .
- for each .
- All values are different.
| # | Score | Constraints |
|---|---|---|
| 1 | 5 | Examples |
| 2 | 15 | , that is, the mayor lives in the last position. |
| 3 | 20 | |
| 4 | 30 | |
| 5 | 30 | No additional limitations. |
Example 1
stdin
100
5 3
15 80 20 50
stdout
18
Explanation
The first sample case is the one described in the task statement.
Example 2
stdin
100
10 5
34 30 16 9 18 14 27 10 15
stdout
5415
Explanation
In the second sample case there are valid combinations. Since we are requested to print only the remainder of the division by , the answer is % = .