Squirrel

A squirrel has discovered a storage with nuts. The storage contains $N$ rows of rooms numbered from $0$ to $N - 1$. The row with index $i$ contains $i + 1$ rooms numbered from $0$ to $i$. The room located in the row $i$ and column $j$ contains $A_{ij}$ nuts.

In the $\frac{N \times (N+1)}{2}$ rooms, the numbers $A_{ij}$ are all distinct and have values between $1$ and $\frac{N \times (N + 1)}{2}$.

Formally, the storage has the shape of a triangle half-matrix, the one located below the main diagonal (including the main diagonal), in which each element represents a number of nuts. The numbers in this half-matrix are the numbers from $1$ to $\frac{N \times (N + 1)}{2}$, with each number appearing exactly once.

For example, for $N = 5$ the storage would have $15$ rooms containing the numbers from $1$ to $15$. An example of such a storage could be the half-matrix shown below:

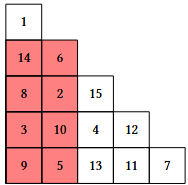
The squirrel walks along the main diagonal, and at each room located at position $(i,i)$ it chooses a single room located in the rectangle with the top-right corner at position $(i,i)$ and the bottom-left corner at position $(N - 1,0)$, and eats the acorns from that room. In the example above, when the squirrel is at position $(1, 1)$, it may choose to eat the nuts from one of the $8$ rooms colored in red. After it has gone through all the rooms on the main diagonal and has eaten the nuts from exactly $N$ different rooms, the squirrel leaves satisfied.

Task

Given $N$ and $A_{i j}$ for any $i$ with $0 \le i < N$ and $j$ with $0 \le j \le i$, find the maximum number of nuts the squirrel can eat.

Also, for each of the $N$ rooms visited, find the number of nuts eaten by the squirrel.

Implementation

You must implement the function

void solve(int N, vector<vector<int>> A, long long& answer, vector<int>& solution)

Function parameters:

Input data:

• int N : storage size / number of rows
• vector<vector<int>> A : Number of nuts in each room (More precisely, in $A_{i,j}$ with $0 \le i < N$ and $0 \le j \le i$ you will find the number of nuts in the room at position $j$ of row $i$)

Output data:

• long long &answer : will contain the maximum number of nuts that the squirrel can eat after going through all $N$ rooms of the diagonal.
• vector<int> &solution : a vector that will contain the amount of nuts eaten by the squirrel in each room. (More precisely, $solution_i$ with $0 \le i < N$ represents the number of nuts eaten by the squirrel when it is in the room $(i,i)$)

ATTENTION!! For both $A$ and $\text{solution}$, the indices start from $0$ and the size of the $solution$ vector should be exactly $N$.

Constraints

• $1 \leq N \le 2 \ 000$
• $1 \leq A_{i j} \leq \frac{N \times (N + 1)}{2}$

Example

input

5
1
14 6
8 2 15
3 10 4 12
9 5 13 11 7

output

64
14 10 15 12 13