In a zoo somewhere in Japan, the zookeepers decided to play the following game with the capybaras:
The capybara enclosure consists of hot springs, which are numbered from to . These hot springs are connected with walkways. Each walkway connects two hot springs, and it is possible to reach any hot spring from any other hot spring by using these walkways. In other words, the capybara enclosure has the structure of a tree (that is, an undirected connected acyclic graph).
Initially, there is at most one capybara in each hot spring, however this can change during the game.
The game consists of several (possibly an infinite number of) rounds. Each round has stages:
- The zookeepers will throw an orange into one of the hot springs. The capybaras will know in which hot spring the orange was thrown into.
- At most one of the capybaras can move to an adjacent hot spring. After that, if there are no capybaras in the hot spring containing the orange, then the zookeepers win and the capybaras lose. Otherwise, the orange is eaten and the game continues.
An initial configuration (that is, the set of hot springs initially containing capybaras) is safe if the zookeepers cannot win the game in a finite number of rounds if both the zookeepers and the capybaras play optimally.
Task
For each from to , find the number of safe initial configurations that have exactly capybaras. Since these numbers can be very large, find their remainders modulo .
Implementation
You will have to implement the following function:
std::vector<int> solve(int N, std::vector<int> U, std::vector<int> V)
This function is called once by the grader and should return a std::vector<int> of length containing the number of safe initial configurations (modulo ) that have exactly capybaras, for every .
The parameters for this function have the following meanings:
- - the number of hot springs.
- - a
std::vector<int>of length which contains the first endpoints of each of the walkways. - - a
std::vector<int>of length which contains the second endpoints of each of the walkways.
For each , the -th walkway connects hot springs and .
Do not forget to include the header file "oranges.h", otherwise you will get a compilation error!
Constraints
- For each walkway ,
- It is guaranteed that the given walkways form a tree (that is, an undirected connected acyclic graph).
| # | Points | Constraints |
|---|---|---|
| 1 | 4 | There exists a hot spring which is directly connected to every other hot spring. |
| 2 | 11 | Each hot spring is directly connected to at most two other hot springs. |
| 3 | 14 | |
| 4 | 9 | |
| 5 | 33 | |
| 6 | 29 | No additional constraints. |
Example 1
input
1
output
0 1
Explanation
The only safe initial configuration is .
Example 2
stdin
4
0 1
1 2
2 3
stdout
0 0 4 4 1
Explanation
The structure of the capybara enclosure in the second example:

There are safe initial configurations with two capybaras: .
All initial configurations that have at least capybaras are safe.
Example 3
stdin
6
0 1
1 2
1 3
0 4
4 5
stdout
0 0 0 0 11 6 1
Explanation
The structure of the capybara enclosure in the third example:
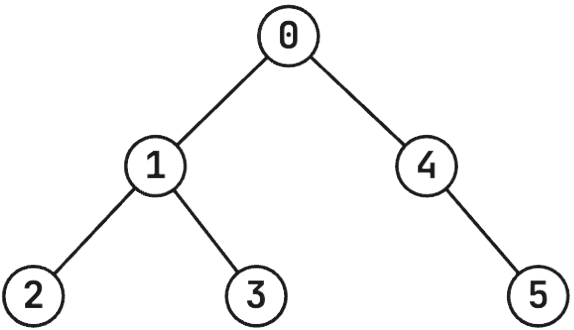
For example, the initial configuration is not safe:
In the first round, the zookeepers will throw an orange into hot spring . The capybara from hot spring is forced to move to hot spring .
In the second round, the zookeepers will throw an orange into hot spring . The capybara from hot spring is forced to move to hot spring .
In the third round, the zookeepers will throw an orange into hot spring . Since there are no capybaras that can move to hot spring , the zookeepers win.
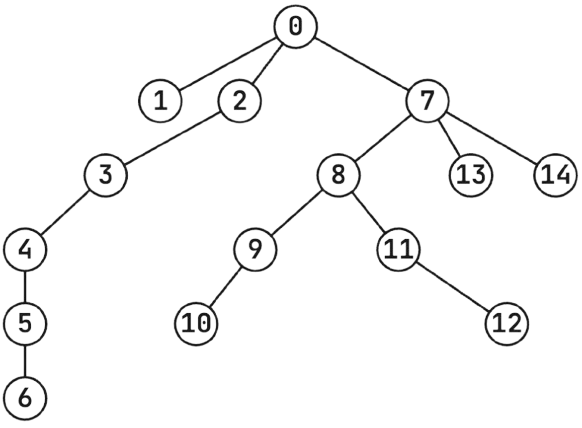
Example 4
stdin
15
0 1
0 2
2 3
3 4
4 5
5 6
0 7
7 8
8 9
9 10
8 11
11 12
7 13
7 14
stdout
0 0 0 0 0 0 0 0 0 560 992 793 361 98 15 1
Explanation
The structure of the capybara enclosure in the fourth example: