It is time for the annual server maintenance at Vianu. Some of the maintenance can be done by humans, but the cables connecting the network are routed through a series of underground pipes that are too small to access! Luckily, a brilliant engineer came up with the idea of letting trained rats check the computers instead.
Each rat can enter the network at one computer, travel along the cables through the underground pipes, and exit at another computer, checking all computers along the way. Because the rats are quite lazy, each rat will only follow a single simple path between its entry and exit point before getting tired.
The maintenance crew wants to have rats check some computers so that among the remaining unchecked ones, the configuration of security codes is "balanced enough". Your task is to determine the minimum number of rats needed.
Task
There are computers, numbered from to , linked through cables. The network is a tree (connected and acyclic).
A single rat can check every computer on the unique simple path between the computer where it enters the network and the computer where it exits. Formally, if a rat enters at computer and exits at computer (), then the rat will check all computers such that:
- and ,
- for all , computers and are directly connected by a cable,
- is minimal.
Rats may reuse the same cables and computers, and a computer can be checked by multiple rats.
Each computer has an associated positive integer code . The maintenance crew fix a maximum acceptable difference . After all rats have done their work, let the set of remaining unchecked computers be . The crew want to ensure that for any pair of .
In other words, the difference between the maximum and minimum code among remaining computers must be at most .
Each rat can only check one path before getting tired. You want to minimize the number of rats used.
Implementation
You should implement the function
int solve(int N, int D, std::vector<int> C, std::vector<int> P, std::vector<int> Q)
This function receives as parameters: , the number of computers, , the maximum acceptable difference, , the codes of the computers, and two vectors of length , and , meaning there is a cable between computers and , for all .
The function should return the minimum number of rats needed so that after all rats have checked their paths, the remaining unchecked computers satisfy
Constraints
- .
- for all .
- .
- , , and all pairs are distinct
| # | Points | Constraints |
|---|---|---|
| 1 | 7 | and for all . |
| 2 | 6 | and for all . |
| 3 | 11 | . |
| 4 | 16 | for all . |
| 5 | 26 | . |
| 6 | 34 | No additional constraints. |
Example 1
input
5 3
1 10 3 8 6
0 1
1 2
2 3
2 4
output
1
Explanation
In the first example, there are computers and . The network can be visualized as:
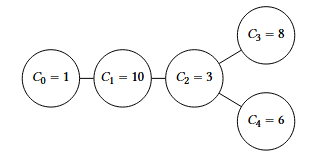
One possible strategy is to send a single rat on a path that starts at computer and exits at computer , passing along the path . After such a path is checked, the network is safe.
Example 2
input
20 30
13 36 11 35 4 9 42 9 1 4 11 3 15 31 46 41 31 17 11 12
19 5
19 0
19 13
19 9
19 4
19 10
5 1
19 18
0 7
5 8
19 12
5 17
13 16
5 14
13 3
19 6
5 15
5 2
4 11
output
3