Palindromic Paths

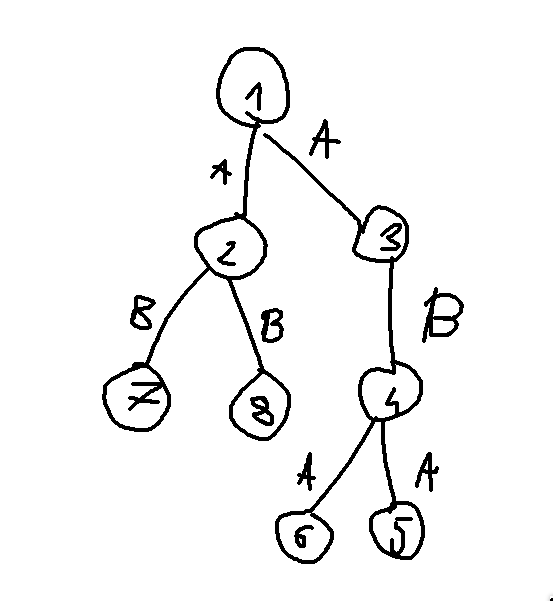
A tree (undirected connected acyclic graph) is given with $N$ nodes and $N−1$ edges, each labeled with a lowercase letter. We will define the path $(x, y)$ as the sequence of edges that lead from node $x$ to node $y$. Additionally, we will consider paths $(x, y)$ and $(y, x)$ to be identical. A path can be palindromic if there exists a way to permute all the letters traversed on that path such that they form a palindromic path.

Task

Determine how many paths can be palindromic.

Input data

The first line contains the number $N$, representing the number of nodes.

The next $N−1$ lines each contain a triplet $a \ b \ ch$, representing an edge connecting node $a$ to node $b$, labeled with the character $ch$.

Output data

Print on one line the number of paths that can be palindromic.

Constraints and clarifications

• $1 \leq N \leq 100 \ 000$

Example

stdin

8
1 2 a
1 3 a
2 7 b
2 8 b
3 4 b
4 5 a
4 6 a

stdout

21

Explanation

The paths that can be palindromic are: $(1, 2)$, $(1, 3)$, $(1, 5)$, $(1, 6)$, $(2, 3)$, $(2, 4)$, $(2, 7)$, $(2, 8)$, $(3, 4)$, $(3, 7)$, $(3, 8)$, $(4, 5)$, $(4, 6)$, $(4, 7)$, $(4, 8)$, $(5, 6)$, $(5, 7)$, $(5, 8)$, $(6, 7)$, $(6, 8)$, $(7, 8)$.