Baby Bob celebrated his birthday recently, and just as you would expect, he received an extraordinary amount of presents from his family. His favorite gift is a coloring book, which contains colorless images that he can fill with colors however he wants to. Baby Bob’s absolute favorite images do not depict childish things like dogs and birds but rather display more abstract objects like triangles, circles, and so on.

Today, Baby Bob has discovered a nice image. The image contains empty circles arranged over the perimeter of a large circle. The circles are numbered from to clockwise. There are line segments connecting circle and circle for each , as well as circle and circle .
Baby Bob liked this picture and decided to modify it a bit. He drew additional straight line segments. These new segments satisfy the following criteria:
- Each new line segment connects two circles that were not connected before.
- No two line segments intersect each other.
- All circles connected by the new segments are distinct, i.e., each circle is connected to *at most one other circle by a new line.
Baby Bob wants to color the circles in his image. He only has crayons of two colors, red and blue. He wants to avoid coloring circles connected by line segments with the same color, but he is mature enough to accept that sometimes he cannot avoid doing so. Instead, he wants to color them such that the numbe of pairs of circles connected by a line segment and having the same color is minimal.
Help Baby Bob by writing a program that finds an optimal coloring of the circles.
Input data
The input file consists of:
- a line containing integers and , the number of circles and the number of extra line segments, respectively.
- lines, the -th of which consisting of integers and , meaning that Baby Bob drew a line segment connecting circle and circle .
Note that the original line segments are not included in the input.
Output data
The output file must contain two lines:
- a line containing a single integer , the minimum number of connected pairs of circles that have the same color in an optimal coloring.
- a line consisting of the integers , the description of an optimal coloring. is if circle should be colored red, and , if it should be colored blue.
If there are multiple optimal colorings, you may output any of them.
Constraints and clarifications
- .
- .
- for each
Your program will be tested against several test cases grouped in subtasks. In order to obtain the score of a subtask, your program needs to correctly solve all of its test cases.
| # | Points | Constraints |
|---|---|---|
| 1 | 0 | Examples |
| 2 | 4 | |
| 3 | 11 | |
| 4 | 8 | |
| 5 | 20 | |
| 6 | 25 | |
| 7 | 32 | No additional limitations |
In each subtask you can obtain a partial score by correctly determining the number of pairs of connected circles having the same color in an optimal coloring.
Specifically, you get of the points of a subtask if the value of is correct in each testcase of the subtask, but there is at least one testcase where the coloring given in the second line of the output contains more than connected pairs with the same color. Note that the second line must contain a valid coloring, that is, numbers with value or , otherwise you may receive an “Output isn’t correct verdict.
Example 1
stdin
5 1
0 2
stdout
1
0 0 1 0 1
Explanation
In the first sample case, the image with the extra line connecting circles and is displayed in the following figure.
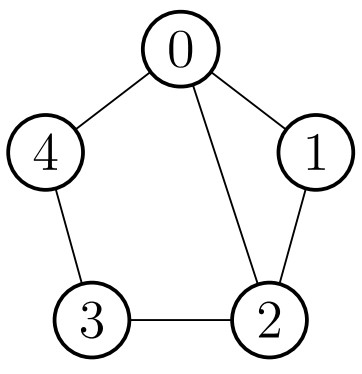
It can be proved that it is not possible to color the circles such that every connected pair has different colors. For example, at least two out of circles and will always have the same color.
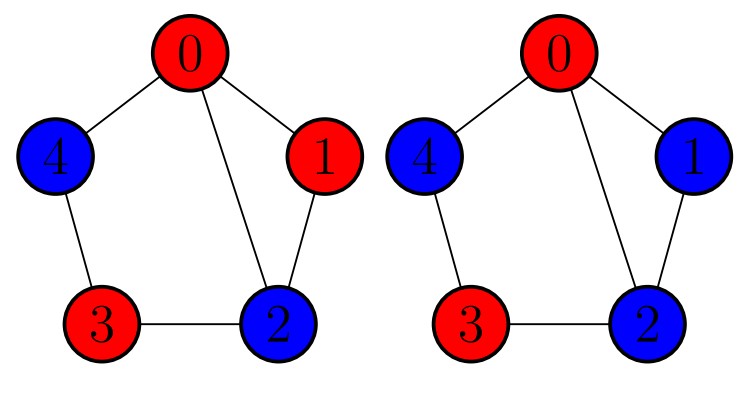
However, it is possible to color the circles such that only one connected pair has the same color. There are exactly four such colorings, two of them are displayed in the figure below.
Example 2
stdin
9 3
1 8
2 4
5 7
stdout
3
0 1 0 1 0 1 1 0 1