Washington Distance

Ethan and George are in Washington D.C. for their favorite debate tournament’s final round. To get to the venue, they need to use a taxi, and the driver expects the directions given according to the city’s unique street system described below. The starting point and destination is an intersection of two streets.

The streets of Washington form a rectangular grid, which can be modeled as vertical and horizontal lines in the planar coordinate system. There is a street parallel to the $Ox$ and $Oy$ axis on each integer coordinate from $−25$ to $25$. However, the streets are numbered in a very strange way.

Firstly, the city is divided into four quadrants: $NW$, $SW$, $NE$, $SE$ (north-west, south-west, north-east, south-east), relative to the center of the city (which corresponds to the origin in the coordinate system). The vertical streets are identified by letters from $A$ to $Z$. Street $A$ goes through the center, and on both the eastern and western sides the streets are named $B$, $C$, ..., $Z$ in the order of distance from the center. The horizontal streets are identified by numbers between $0$ and $25$. Street $0$ goes through the center, and in both the northern and southern halves, the streets are numbered from the bottom to the top with increasing numbers from $1$ to $25$ (so the numbers reflect the remainder of the real coordinate when divided by $26$). See the image below for a better understanding.

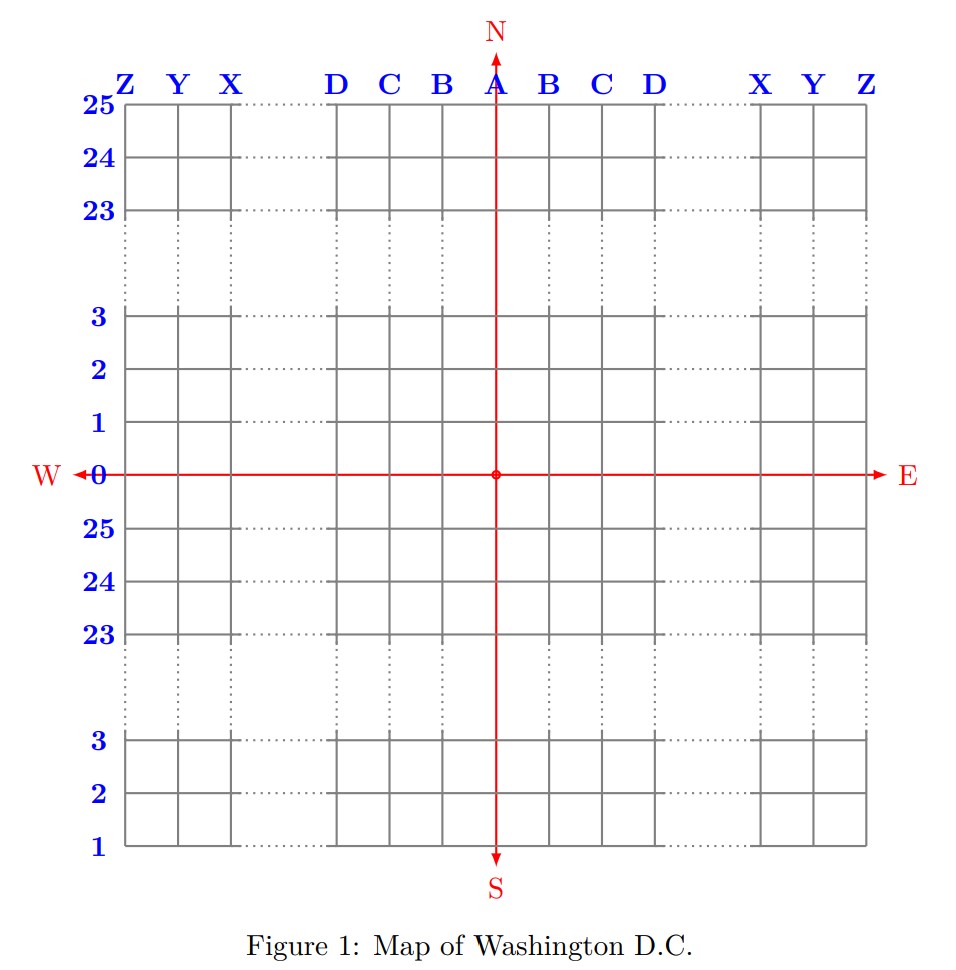
Now, knowing this, Ethan and George want to know the distance between $T$ pairs of points, according to the Washington Coordinate system. The distance means the length of the ride with the taxi, which can only travel along the streets, given in units of the coordinate system.

Input data

The first line of the input contains $T$, the number of test cases $(1 \leq T \leq 10^4)$.
The next $T$ lines of the input contain two addresses according to the Washington Coordinate System, given by their direction, letter and street number.

Output data

You need to write a single line with an integer: the unique integer that solves this task.

Constraints and clarifications

• $1 \leq T \leq 10^4$;

Your program will be tested against several test cases grouped in subtasks. In order to obtain the score of a subtask, your program needs to correctly solve all of its test cases.

Example

stdin

5
NE A 5 NE B 7
NE G 15 SW P 0
SE U 5 NW Q 10
NW A 19 SW B 3
SE Q 21 SW P 4

stdout

3
36
67
43
48

Explanation

The situation of the first sample case can be seen below: (clearly the distance is $3$)

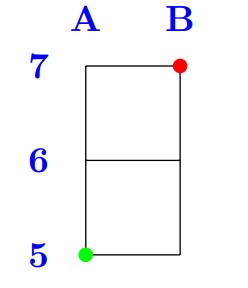
In the second sample case the taxi driver does not have to cross line $0$, but must cross line $A$. The distance between line $G$ (corresponding to the starting point) and line $A$ is $6$. The distance between line $P$ (corresponding to the end point) and line $A$ is $15$. So the total distance is $6 + 15 + 15 = 36$.

In the third sample case the taxi driver must cross both line $0$ and line $A$. The distance between line $U$ (corresponding to the starting point) and line $A$ is $20$. The distance between line $Q$ (corresponding to the end point) and line $A$ is $16$. So the total distance is $20 + 16 + 21 + 10 = 67$ as the distance between line $5$ (corresponding to the starting point) and line $0$ is $21$.