Robotics

Ne aflăm în secția de vopsitorie a uzinei Toyota Motor unde inginerii japonezi prezintă ultimul tip de robot industrial de vopsire. În dorința de a evidenția calitatea și viteza de execuție a roboților, inginerii folosesc pentru demonstrație o tablă de dimensiunea $n×n$, împărțită în pătrate cu latura egală cu $1$, reprezentată sub forma unui tablou bidimensional cu $n$ linii şi $n$ coloane.
Un robot utilizat pentru vopsire are două brațe telescopice care se deplasează de-a lungul unei axe. Fiecare braț poate vopsi într-o unitate de timp un singur pătrat. La momentul de timp $t=0$ robotul primește comanda de a se poziționa într-un pătrat specificat prin coordonatele $(x$, $y)$. În funcție de traiectoria de deplasare roboții folosiți sunt de două tipuri. La momentul de timp $t$ robotul de tip $1$ vopsește pătratele aflate la coordonatele: $(x-t$, $y+t)$ și $(x+t$, $y-t)$, iar robotul de tip $2$ vopsește pătratele aflate la coordonatele: $(x+t$, $y+t)$ și $(x-t$, $y-t)$. Pentru vopsirea unui pătrat se consumă $1$ litru de vopsea. Pe tablă sunt așezați $m$ roboți.

Cerinţe

Cunoscând pentru cei $m$ roboți coordonatele inițiale $(x_{i} \ ,y_{i})$, $i=1$, $2$, …, $m$, se cere să se determine:

1. Cantitatea totală de vopsea care a fost folosită de roboți după $t$ unități de timp
2. Numărul minim de unități de timp necesare formării primului dreptunghi cu arie nenulă. Un dreptunghi corect format este rezultatul intersecției a două traiectorii paralele a doi roboți de tip $1$ cu două traiectorii paralele a doi roboți de tip $2$, iar colțurile dreptunghiului sunt $4$ pătrate care au fost vopsite de doi roboți de tipuri diferite.

Date de intrare

Fişierul de intrare robotics.in conţine pe prima linie trei valori naturale nenule $n$, $m$ și $t$, cu semnificațiile din enunț, despărțite prin câte un singur spațiu. Pe fiecare dintre următoarele $m$ linii se află câte trei valori naturale nenule $x_{i}$, $y_{i}$ și $z_{i}$, despărțite prin câte un spațiu, unde: $x_{i}$, $y_{i}$ reprezintă coordonatele inițiale unde se poziționează robotul $i$, iar $z_{i}$ reprezintă tipul robotului.

Date de ieșire

Fişierul de ieşire robotics.out va avea două linii.
Prima linie conține un număr natural $C$ nenul ce reprezintă cantitatea totală de vopsea care este folosită de roboți după $t$ unități de timp.
A doua linie conține un număr natural nenul $Tmin$ ce reprezintă numărul minim de unități de timp necesare formării primului dreptunghi de arie nenulă.

Restricții și precizări

• $1 \leq t < n \leq 1 \ 000$
• $1 \leq m \leq 2 \cdot n$
• $1 \leq x, \ y \leq n$
• Coordonatele celor $m$ roboți sunt distincte două câte două.
• Doi roboți nu se pot afla pe aceeași traiectorie la un moment dat.
• La momentul $t=0$ robotul se poziționează în pătratul specificat prin coordonatele $(x, y)$ și vopsește o singură dată acest pătrat.
• Doi roboți de tipuri diferite care ajung în același timp pe un pătrat pot vopsi simultan pătratul.
• Dacă brațul unui robot părăsește tabla dreptunghiulară, brațul își încetează activitatea.
• Pentru rezolvarea corectă a primei cerinţe se acordă $20$ de puncte, iar pentru cerința a doua se acordă $80$ de puncte.

Exemplul 1

robotics.in

13 3 6
3 5 1
7 5 2
7 9 1

robotics.out

29
0

Explicație

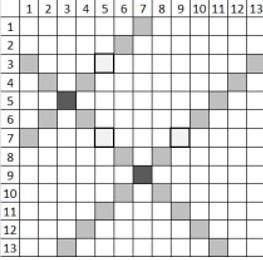
Cantitatea de vopsea care este folosită de roboți după $t$ unități de timp este $29$. Nu se pot forma dreptunghiuri.

Exemplul 2

robotics.in

19 9 4
4 5 1
4 14 2
2 11 1
14 7 2
5 10 2
14 13 1
7 4 2
7 10 1
12 13 2

robotics.out

75
3

Explicație

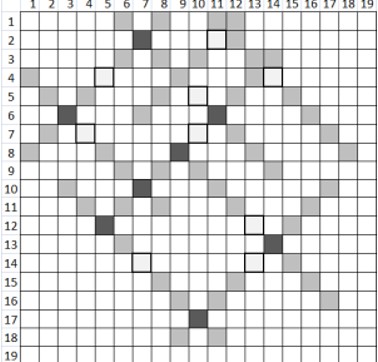
Cantitatea de vopsea care este folosită de roboți după $t$ unități de timp este $75$.
Singurele dreptunghiuri corect formate după $t=4$ au colțurile în pătratele de coordonate: ($2$, $7$), ($6$, $11$), ($10$, $7$), ($6$, $3$), respectiv ($8$, $9$), ($13$, $14$), ($17$, $10$), ($12$, $5$).
Observăm faptul că primul dreptunghi se formează după $t=3$ (timpul minim)