fence

Un proprietar vinde un teren de formă dreptunghiulară împărțit în $M \times N$ parcele de formă pătrată cu lungimea laturii de o unitate. Fiecare parcelă costă $V$ lei. Vlad s-a interesat și a aflat pentru fiecare din parcelele terenului care este valoarea de revânzare. El constată că unele parcele i-ar putea aduce profit, iar altele i-ar aduce pierdere. Fiind isteț, negociază cu proprietarul să cumpere atâtea parcele de teren câte pot fi împrejmuite cu un singur gard de lungime egală cu $2M+2N$ unități. Terenul are pe fiecare din cele patru laturi acces la drumul exterior, pe o porțiune de lungime egală cu o unitate. Vlad negociază astfel încât terenul achiziționat să conțină și cele patru parcele de acces la exterior.

Cerință

Cunoscând $M$ și $N$ — dimensiunile terenului, valorile de revânzare pentru fiecare parcelă din teren, $V$ — prețul de cumpărare al fiecărei parcele și $x_{nord}$, $x_{sud}$, $y_{vest}$ și $y_{est}$ — pozițiile parcelelor cu acces la drumul exterior, să se determine:

1. Profitul $P_{\text{arie\_minimă}}$ pe care-l poate obține Vlad după cumpărarea și apoi revânzarea suprafeței de teren de arie minimă, împrejmuită conform condițiilor negociate.
2. Profitul maxim $P_{\text{max}}$ pe care-l poate obține Vlad după cumpărarea și apoi revânzarea unei suprafețe de teren împrejmuită conform condițiilor negociate.

Date de intrare

Fișierul fence.in conține pe prima linie numărul $t$.
Pentru toate testele de intrare numărul $t$ poate avea doar valoarea $1$ sau valoarea $2$.
Pe linia a doua se găsesc numerele $M$, $N$, $V$, $x_{nord}$, $x_{sud}$, $y_{vest}$ și $y_{est}$ separate prin câte un spațiu, iar pe următoarele $M$ linii se află câte $N$ numere naturale separate prin câte un spațiu, reprezentând valorile de revânzare ale celor $M \cdot N$ parcele de teren.

Date de ieșire

Dacă valoarea lui $t$ este $1$, atunci se va rezolva numai cerința 1.
În acest caz în fișierul de ieșire fence.out se va scrie pe prima linie numărul $P_{\text{arie\_minimă}}$.
Dacă valoarea lui $t$ este $2$, atunci se va rezolva numai cerința 2.
În acest caz în fișierul de ieșire fence.out se va scrie pe prima linie numărul $P_{\text{max}}$.

Restricții și precizări

• $3 \leq M, N \leq 1\ 000$
• $1\ 000 \leq V \leq 10\ 000$
• $2 \leq x_{nord}, x_{sud} \leq N-1$
• $2 \leq y_{vest}, y_{est} \leq M-1$
• $(x_{nord} - x_{sud}) \cdot (y_{est} - y_{vest}) \geq 0$
• Valoarea de revânzare a oricărei parcele din teren este un număr natural din intervalul $[1, 20\ 000]$.
• Prin profit se înțelege suma valorilor de revânzare corespunzătoare parcelelor din suprafața împrejmuită din care se scade produsul dintre prețul de cumpărare $V$ și numărul parcelelor împrejmuite, care poate fi și negativ.
• Pentru rezolvarea corectă a primei cerințe se va obține $20\%$ din punctaj.
• Cerința 2 conține teste în valoare de 30 de puncte pentru care se îndeplinește condiția $M, N \leq 15$.

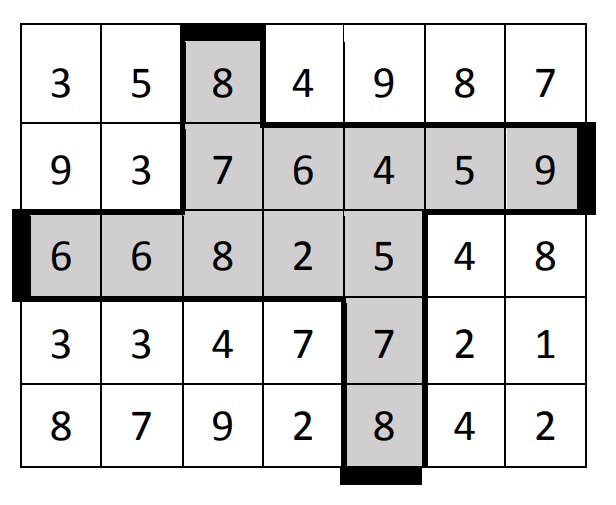
Exemplul 1

fence.in

1
5 7 6 3 5 3 2
3 5 8 4 9 8 7
9 3 7 6 4 5 9
6 6 8 2 5 4 8
3 3 4 7 7 2 1
8 7 9 2 8 4 2

fence.out

3

Explicație

$M=5$, $N=7$, $V=6$, $x_{nord}=3$, $x_{sud}=5$, $y_{vest}=3$, $y_{est}=2$

$P_{\text{arie\_minimă}} = (8+7+6+4+5+9+6+6+8+2+5+7+8) - 6 \cdot 13 = 81-78 = 3$

Exemplul 2

fence.in

2
5 7 6 3 5 3 2
3 5 8 4 9 8 7
9 3 7 6 4 5 9
6 6 8 2 5 4 8
3 3 4 7 7 2 1
8 7 9 2 8 4 2

fence.out

8

Explicație

$M=5$, $N=7$, $V=6$, $x_{nord}=3$, $x_{sud}=5$, $y_{vest}=3$, $y_{est}=2$

$P_{\text{max}} = (8+4+9+8+7+7+6+4+5+9+6+6+8+2+5+7+7+8) - 6 \cdot 18 = 116 - 108 = 8$