Ben are un teren pe care se află o pădure cu arbori seculari. Acolo vrea să-şi construiască o cabană, însă el fiind ecologist nu vrea să taie niciun arbore, ci vrea să găsească cea mai mare suprafaţă dreptunghiulară fără arbori. El caută o suprafaţă dreptunghiulară străjuită doar în colţuri de arbori şi cu laturile paralele cu axele de coordonate. Ben cunoaşte coordonatele tuturor arborilor din pădure şi vă roagă să-l ajutaţi să găsească aria dreptunghiului cu suprafaţă maximă care are arbori doar în cele patru colțuri.
Cerinţă
Cunoscând numărul arborilor din pădure şi coordonatele acestora, se cere să se determine aria dreptunghiului de suprafaţă maximă cu copaci doar în cele 4 colţuri, unde Ben intenţionează să-şi construiască cabana.
Date de intrare
Fişierul de intrare cabana.in conţine pe prima linie un număr natural , reprezentând numărul de arbori din pădure. Pe fiecare dintre următoarele linii se află două numere întregi, separate printr-un spațiu, ce reprezintă abscisa și ordonata unui arbore.
Date de ieşire
În fişierul de ieşire cabana.out se scrie pe prima linie numărul natural , reprezentând aria dreptunghiului de suprafață maximă.
Restricţii şi precizări
- Pentru din teste: și .
- Pentru din teste: și .
- Pentru din teste: și .
- Pentru din teste: și .
- Pentru din teste: și .
- Nu există doi arbori așezați pe aceeași poziție.
Exemplu
cabana.in
22
6 25
25 22
15 5
23 23
6 7
11 16
11 20
10 22
6 16
12 6
7 19
10 19
10 14
7 14
7 7
18 14
18 7
10 7
19 19
29 19
29 4
19 4
cabana.out
150
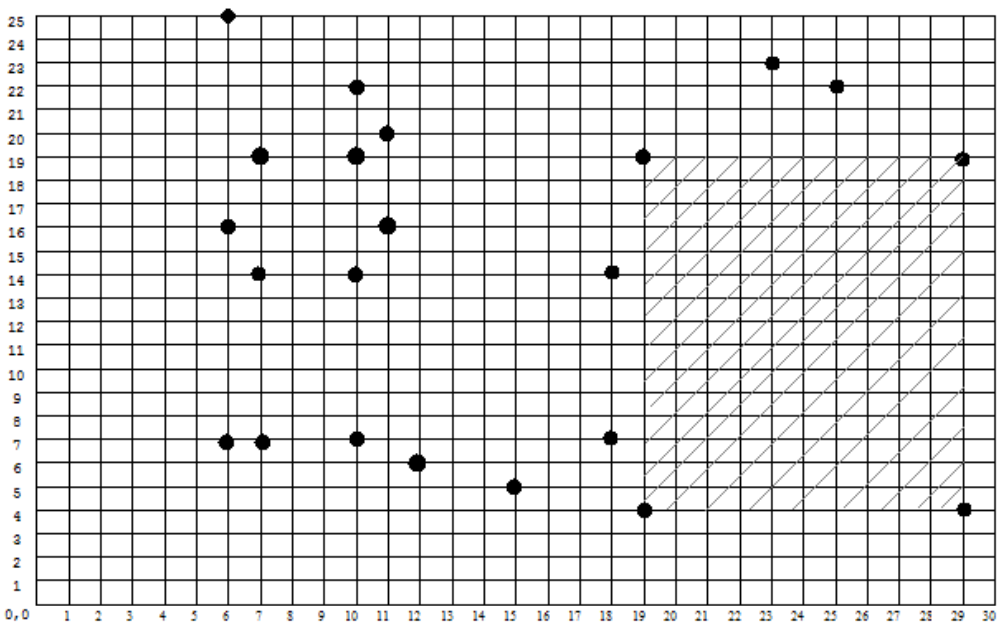
Explicație
Coordonatele dreptunghiului de arie maximă cu laturile paralele cu axele de coordonate şi care nu conţine arbori decât în colţuri sunt , , , , deci aria maximă este .