tunel

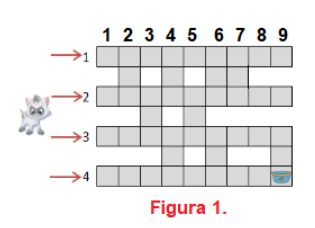
Tommy este un motan alintat care adoră să se plimbe prin orice tunel. De aceea, stăpânii lui i-au construit o nouă jucărie, formată din $N$ tuneluri interconectate (etichetate cu numerele distincte de la $1$ la $N$. Toate tunelurile au aceeași lungime, sunt formate din $M$ elemente unitare identice (numerotate cu numerele distincte de la $1$ la $M$) și au ieșiri la ambele capete. Conectarea dintre două tuneluri alăturate se face printr-un element unitar numit pasaj. În exemplul din Figura $1$, jucăria este formată din $4$ tuneluri, fiecare tunel fiind format din $9$ elemente unitare.

Pentru a fi mai provocator, stăpânii motanului plasează în ultimul element unitar al ultimului tunel o recompensă.

Motan isteț, Tommy a învățat deja toate regulile jocului:

• poate intra prin capătul din stânga al oricărui tunel (prin elementul unitar 1);
• nu trece de multe ori prin același pasaj;
• dacă nu se află lângă un pasaj, continuă să meargă prin tunel către dreapta;
• dacă ajunge la un pasaj, atunci trece prin acesta în tunelul alăturat;
• dacă ajunge în ultimul element unitar al tunelului etichetat cu $N$, atunci Tommy iese din acest tunel cu recompensă, chiar dacă ar exista un pasaj ce conectează acest ultim element la ultimul element din tunelul $N - 1$ (vezi Figura 2.b);
• dacă ajunge în ultimul element unitar al tunelului etichetat cu $N - 1$ și există un pasaj care conectează acest element cu ultimul element unitar al tunelului etichetat cu $N$, atunci Tommy trece prin acest pasaj în ultimul element din ultimul tunel, ia recompensa și iese din tunel Figura 2.a). În cazul în care acest pasaj nu există, Tommy iese din tunelul $N - 1$ fără recompensă;
• dacă ajunge în ultimul element unitar al unui tunel cu eticheta mai mică decât $N - 1$, atunci Tommy iese din tunel fără recompensă.

Ajutați-l pe Tommy să ajungă cât mai repede la recompensă respectând regulile jocului!

Cerință

Scrieţi un program care citește numerele naturale $N, M și X$, iar apoi determină:

• eticheta tunelului prin care iese Tommy dacă intră în tunelul cu eticheta $X$ respectând regulile jocului;
• numărul $L$ de elemente unitare (ale tunelurilor și ale pasajelor) prin care Tommy ar trebui să treacă, respectând regulile jocului, pentru a ajunge la recompensă.

Date de intrare

Fișierul tunel.in conține pe prima linie un număr natural $C$ reprezentând cerința din problemă care trebuie rezolvată $1$ sau $2$.

A doua linie a fișierului conține cele trei numere naturale $N, M și X$, separate prin câte un spațiu, cu semnificația din enunț. Următoarele $N - 1$ linii descriu pasajele dintre tuneluri. Prima linie dintre cele $N - 1$ indică pasajele dintre tunelurile etichetate cu $1$ și $2$, următoarea linie indică pasajele dintre tunelurile etichetate cu $2$ și $3$, $\dots$, ultima dintre cele $N - 1$ linii indică pasajele dintre tunelurile etichetate cu $N - 1$ și $N$.

Primul număr din fiecare astfel de linie reprezintă numărul $P$ de pasaje, iar următoarele $P$ numere distincte, scrise în ordine crescătoare, reprezintă pozițiile elementelor unitare (dintre cele două tuneluri) conectate prin cele $P$ pasaje.

Date de ieșire

Dacă $C = 1$, fișierul tunel.out va conține pe prima linie un număr natural reprezentând răspunsul la cerința $1$.

Dacă $C = 2$, fișierul tunel.out va conține pe prima linie numărul natural $L$ reprezentând răspunsul la cerința $2$.

Restricții și precizări

• $3 \leq N \leq 1 \ 000$;
• $4 \leq M \leq 20 \ 000$;
• $1 \leq P \leq M−2$;
• Pot exista cel mult $150 \ 000$ pasaje care interconectează tunelurile.
• Pot exista pasaje învecinate care să conecteze elementele unitare din două tuneluri alăturate (vezi Figura $1$) în care tunelurile $1$ și $2$ sunt interconectate prin pasajele învecinate dintre elementele $6$, respectiv $7$).
• Primul element unitar din fiecare tunel nu este conectat la niciun pasaj.
• Ultimul element unitar din tunelurile etichetate cu $1, 2, \dots, N - 2$ nu este conectat la niciun pasaj.
• Oricare element unitar poate fi conectat la cel mult un pasaj.
• Oricare două tuneluri etichetate cu numere consecutive sunt interconectate prin cel puțin un pasaj.
• Pentru fiecare intrare într-un tunel există traseu către ieșire.
• Pentru fiecare test există cel puțin o intrare într-un tunel prin care Tommy poate ajunge la ieșirea cu recompensă din tunelul $N$.
• Pentru cerința $1$ se acordă $40$ de puncte. iar pentru cerința $2$ se acordă $60$ de puncte.

Exemplul 1

tunel.in

1
4 9 4
3 2 4 6
2 3 5
3 4 6 9

tunel.out

1

Explicație

Se rezolvă cerința $1$. $N = 4$, $M = 9$, $X = 4$.

Tommy, intra prin tunelul etichetat cu $X = 4$ și iese prin tunelul etichetat cu $1$ (vezi Figura $2$.d).

Exemplul 2

tunel.in

2
4 9 4
3 2 4 6
2 3 5
3 4 6 9

tunel.out

17

Explicație

Se rezolvă cerința $2$. $N = 4, M = 9, X = 4$. Figurile $2$.a, $2$.b, $2$.c, $2$.d conțin trecerea lui Tommy prin tunele pentru fiecare din cele patru intrări. Doar $2$ dintre aceste treceri îl duc pe Tommy la recompensă (vezi Figura $2$.a și Figura $2$.b). Dacă Tommy intră prin tunelul $2$ atunci el ajunge la recompensă trecând prin numărul minim $L = 17 = min(17,19)$ elemente unitare.