Fermierul Feder cultivă cartofi pe un teren dreptunghiular de lățime metri și lungime metri, compartimentat în zone pătratice identice de lungime metru, dispuse alăturat, câte pe lățime (pe linii, numerotate de la la ) și câte pe lungime (pe coloane, numerotate de la la ).
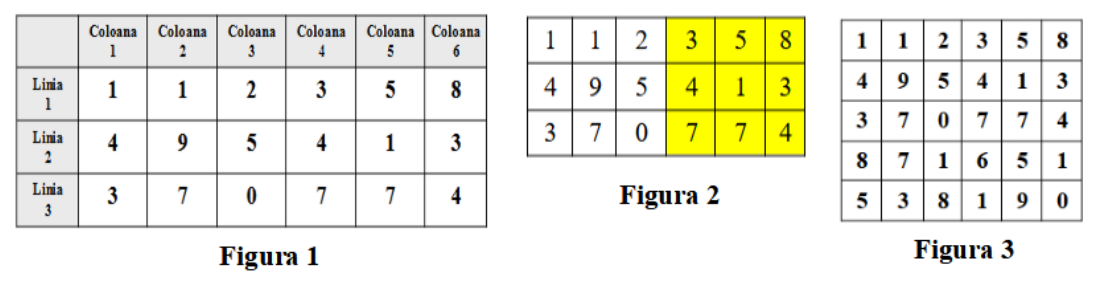
În fiecare zonă pătratică se află câte o plantă de cartofi. Parcurgând terenul de la prima linie către ultima, fiecare linie cu număr impar parcurgând-o de la coloana către coloana , iar fiecare linie cu număr par parcurgând-o de la coloana către coloana , fermierul (pasionat de matematică) a scris numerele cartofilor produși de fiecare plantă, în ordinea parcurgerii, și a constatat că a obținut șirul cifrelor unităților primilor termeni ai șirului Fibonacci (vezi Figura în care și ).
Cerință
Scrieți un program care citește numerele și (cu semnificația din enunț), iar apoi determină:
- numărul plantelor din teren care nu au produs niciun cartof;
- numărul maxim de cartofi care pot fi produși de plantele dintr-o suprafață pătratică din terenul fermierului;
- pentru fiecare dintre cele perechi de numere () citite, numărul cartofilor produși de plantele aflate în zonele pătratice situate între coloanele cu numerele și , inclusiv acestea.
Date de intrare
Fișierul de intrare cartofi.in conține pe prima linie un număr natural reprezentând cerința din problemă care trebuie rezolvată (, sau ). A doua linie a fișierului conține cele două numere naturale și , separate printr-un spațiu, cu semnificația din enunț. Dacă , atunci fișierul va mai conține pe a treia linie numărul natural , iar pe fiecare linie dintre următoarele , câte două numere naturale separate printr-un spațiu reprezentând câte o pereche de numere () dintre cele .
Date de ieșire
Fișierul de ieșire cartofi.out va conține:
Dacă , pe prima linie un număr natural reprezentând răspunsul la cerința .
Dacă , pe prima linie un număr natural reprezentând răspunsul la cerința .
Dacă , linii, câte o linie pentru fiecare pereche () dintre cele . Linia corespunzătoare fiecărei perechi () va conține un număr natural reprezentând numărul cartofilor produși de plantele aflate în zonele pătratice situate între coloanele cu numerele și , inclusiv aceste valori, reprezentând răspunsul la cerința .
Restricții și precizări
- ;
- ;
- ;
- ;
- ;
- Pentru cerința 1 se acordă de puncte, iar pentru cerințele și se acordă câte de puncte.
- Șirul Fibonacci este definit astfel: , și , dacă , ( este un număr natural nenul).
- O suprafață pătratică din teren este formată din zone pătratice alăturate dispuse câte pe linie și câte pe coloană, oricare ar fi ;
Exemplul 1
cartofi.in
1
3 6
cartofi.out
1
Explicație
Se rezolvă cerința . , . Primii = termeni ai șirului Fibonacci sunt: . Astfel, numerele cartofilor produși de fiecare plantă din teren sunt cele din Figura . În teren există o singură plantă care nu a produs niciun cartof (cea din linia , coloana ).
Exemplul 2
cartofi.in
2
3 6
cartofi.out
42
Explicație
Se rezolvă cerința . , . Numerele cartofilor produși de fiecare plantă din teren sunt cele din tabelul din Figura . Plantele aflate în suprafața pătratică galbenă din tabelul din Figura au produs cel mai mare număr de cartofi.
Exemplul 3
cartofi.in
3
5 6
3
1 2
4 6
2 3
cartofi.out
48
64
43
Explicație
Se rezolvă cerința . , , . Tabelul din Figura conține numerele cartofilor produși de fiecare plantă din teren sunt cele din Figura . Suma elementelor cuprinse între coloanele (), inclusiv și , este . Suma elementelor cuprinse între coloanele (), inclusiv și , este . Suma elementelor cuprinse între coloanele (), inclusiv și , este .