Jocul betasah se joacă folosindu-se doar piese asemănătoare damelor clasicului șah, numite tot dame. Suprafața de joc are o formă triunghiulară și este formată din pătrate identice dispuse pe rânduri și coloane. Rândurile se numerotează de sus in jos, de la la . Coloanele se numerotează de la stânga la dreapta, de la la . Primul rând conține un singur pătrat, al doilea rând conține două pătrate alăturate, , al -lea rând conține pâtrate alăturate, ca în suprafețele de joc cu din figurile de mai jos. Din cele pătrate, sunt gri, iar restul sunt albe. Poziția fiecărui pătrat de pe suprafața de joc este dată de rândul și coloana în care acesta este situat.
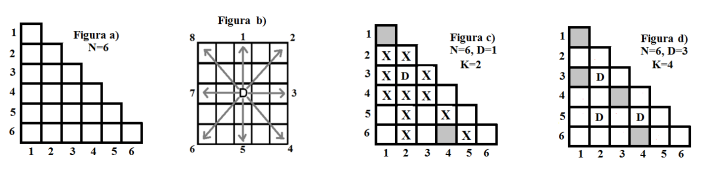
Pe suprafața de joc sunt așezate dame în pătrate albe distincte, ocupându-le. Într-un pătrat alb poate fi așezată o singură damă, iar într-un pătrat gri nu poate fi așezată nicio damă. Poziția unei dame pe suprafața de joc este dată de poziția pătratului alb în care este așezată dama.
Damele pot accesa orice pătrat alb neocupat situat pe direcțiile: verticală, orizontală sau diagonală, numerotate de la la în figura ). Accesul pe o direcție se face trecând din pătrat alb în pătrat alb (doar pătrate albe neocupate) până la întâlnirea unui pătrat gri sau a unui pătrat alb ocupat de o altă damă sau până la terminarea suprafeței de joc.
Numim pătrat accesibil orice pătrat alb neocupat (de pe suprafața de joc) care ar putea fi accesat de cel puțin una din cele dame.
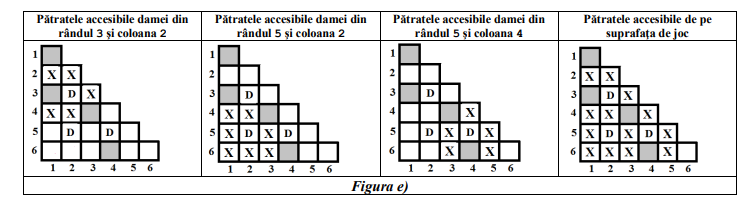
De exemplu, pentru suprafața de joc din figura ) numărul de pătrate accesibile (marcate cu ) de pe suprafață este ; pentru suprafața de joc cu și din figura ) numărul de pătrate accesibile de pe suprafață este . În figura ) sunt marcate cu pătratele accesibile fiecărei dame de pe suprafața de joc din figura ).
Cerință
Scrieți un program care să citească numerele naturale , pozițiile damelor și ale pătratelor gri pe suprafața de joc și care să determine:
- numărul maxim de pătrate albe conținute de un rând al suprafeței de joc;
- numărul de pătrate accesibile de pe suprafața de joc.
Date de intrare
Fișierul de intrare betasah.in conține:
- pe prima linie cele trei numere naturale , separate prin câte un spațiu, cu semnificația din enunț;
- pe linia două numere naturale nenule , separate prin câte un spațiu, reprezentând poziția damei pe suprafața de joc (rândul și coloana ), pentru ;
- pe linia două numere naturale nenule , separate printr-un singur spațiu, reprezentând poziția pătratului gri pe suprafața de joc (rândul și coloana ), pentru .
Date de ieșire
Fișierul de ieșire betasah.out va conține pe prima linie numărul natural și pe a doua linie numărul natural , cu semnificația din enunț. Pentru obținerea punctajelor parțiale, trebuie respectat acest format.
Restricții și precizări
- ;
- ;
- ;
- ;
- ;
- ;
- pentru rezolvarea corectă a cerinței ) se acordă din punctaj, iar pentru rezolvarea corectă a cerinței ) se acordă din punctaj.
Exemplu
betasah.in
6 3 4
3 2
5 2
5 4
3 1
4 3
6 4
1 1
betasah.out
5
13
Explicație
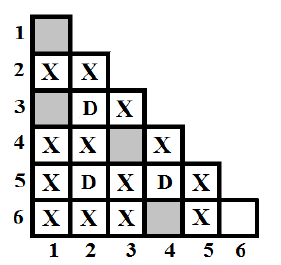
.
Rândurile și conțin numărul maxim de pătrate albe.
Numărul de pătrate accesibile de pe suprafața de joc este .
În desenul alăturat corespunzător suprafeței date, cele pătrate accesibile sunt marcate cu .
Astfel, pe prima linie a fișierului betasah.out se va scrie numarul , iar pe a doua linie a fișierului se va scrie numărul .