Grafuri

Un graf neorientat se numește bipartit dacă mulțimea tuturor nodurilor sale poate fi împărțită în două submulțimi disjuncte astfel încât orice muchie să aibă o extremitate între-o submulțime și cealaltă extremitate în cealaltă submulțime. Numim graf ciclu un graf în care nodurile sunt etichetate cu numere naturale distincte, să le spunem $e_1, e_2, ..., e_k$ și avem exact muchiile: $e_1 - e_2, e_2 - e_3, ... , e_k - e_1$. De asemenea, etichetele respectă ordinea $e_1 < e_2 < ... < e_k$. Altfel spus, graful ciclu are toate nodurile și toate muchiile dispuse încât să formeze un ciclu. Se dau mai multe grafuri ciclu și se cere formarea unui graf bipartit utilizându-le cu respectarea următoarelor reguli:

• Dacă primul graf ciclu are $x$ noduri și al doilea are $y$ noduri, etichetele nodurilor primului graf sunt considerate de la $1$ la $x$ iar ale celui de-al doilea graf sunt considerate de la $x + 1$ la $x + y$. Etichetarea nodurilor următoarelorarelor grafuri ciclu date se face similar, folosind numere consecutive continuând cu prima etichetă disponibilă de la graful anterior.
• Graful bipartit trebuie format din grafurile ciclu date, considerându-le pe acestea în ordinea de la intrare.
• Graful ciclu curent se alipește la graful format anterior prin suprapunerea unei muchii a sa peste o muchie a ultimului graf ciclu alipit. în momentul suprapunerii, avem următoarele două variante: muchia nouă (formată deci din cele două suprapuse) se păstrează mai departe sau se elimină.
• Explicăm mai departe modul de suprapunere a două muchii. Muchia m1 o considerăm etichetată cu $v_1 - v_2$ iar muchia $m_2$ o considerăm etichetată cu $v_3 - v_4$. Considerăm $v_1 < v_2 < v_3 < v_4$. Nodul $v_2$ se va suprapune peste nodul $v_4$ iar nodul $v_1$ peste nodul $v_3$. Noile noduri vor avea mai departe etichetele $v_1$ și $v_2$. Pe scurț nodurile cu eticheta mai mare de la $m_1$ și $m_2$ se vor suprapune (și eticheta care rămâne mai departe este cea mai mică dintre ele) și similar pentru celelalte două.
• La alipirea grafului ciclu nou se va proceda astfel: de la el se alege muchia formată cu cele două etichete maxime. Se alege o muchie care aparț ine grafului ciclu alipit anterior, dacă aici sunt mai multe variante, se alege muchia ce conț ine nodul cu eticheta maximă în acel momenț iar dintre cele două care conț in acea etichetă, se alege cea care are cealaltă etichetă cu valoarea mai mare.

Date de intrare

Prima linie a fișierului de intrare va conține un număr $n$ ce reprezintă numărul de grafuri ciclu date. Linia a doua conține $n$ numere reprezentând, în ordine, numărul de noduri ale fiecărui graf ciclu.

Date de ieșire

Pe prima linie a fișierului de ieșire se va scrie $m$, reprezentând numărul minim de muchii suprapuse care trebuie eliminate pentru a obț ine un graf bipartit. Pe linia a doua și a treia se găsesc respectiv etichetele nodurilor componente ale celor două submulțimi care descriu graful bipartit, separate prin spațiu și în ordine crescătoare în cadrul aceleiași linii. Prima dintre cele două linii conține eticheta $1$ (se observă că pe parcursul aplicării alipirilor în mulțimea etichetelor rămase nu se mai regăsesc neapărat toate numerele de la $1$ la $n$, dar numărul $1$ va rămâne). Dacă problema nu are soluție, la ieșire se va scrie doar numărul $−1$.

Restricții

• $1 ≤ n ≤ 1 \ 000$
• grafurile ciclu date pot avea între $3$ și $100$ de noduri
• dacă la alipirea grafului ciclu curent muchia obținută nu s-a eliminat, ea nu va putea fi folosită la altă alipire ulterioară.

Subtask 1 (10 puncte)

• $n = 1$.

Subtask 2 (15 puncte)

• Toate grafurile ciclu au $3$ noduri.

Subtask 3 (15 puncte)

• Toate grafurile ciclu au $4$ noduri.

Subtask 4 (60 puncte)

• Fără alte restricții.

Exemplu

stdin

3
3 3 4

stdout

1
1 4 8
2 3 7

Explicații

• Conform explicațiilor din enunț, grafurile ciclu date în exemplul de mai sus sunt inițial etichetate astfel:
  
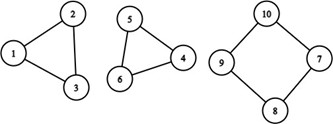
• Pornim cu primul graf ciclu și i-l alipim pe al doilea. Muchia suprapusă se va elimina.
  
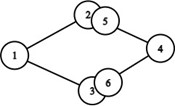
• Adăugăm acum al treilea graf ciclu și trebuie să facem suprapunerea ca în desenul de mai jos. De această dată decidem să nu mai eliminăm muchia.
  
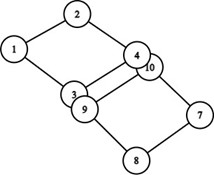
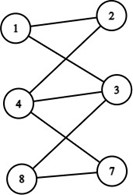
• Graful obținut este:
  
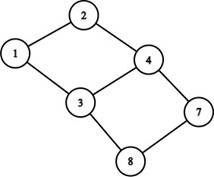
• îl observăm mai ușor ca graf bipartit vizualizându-l astfel: