Fie un număr natural N și o încăpere de lungime 2 * N + 2 văzută ca un interval închis [-N - 1, N + 1]. În centrul C al camerei (C = 0), se află inițial o balerină pe nume Costelina Salopeta. Ea urmează să efectueze T pași de dans de lungime 1, făcând primul pas spre dreapta. În cele 2 * N puncte distincte de coordonate întregi din interiorul camerei se pot plasa K obstacole. Atunci când balerina ajunge într-un punct cu obstacol, ea se împiedică şi face o piruetă. Astfel ea își schimbă sensul de mişcare, iar obstacolul din punctul respectiv dispare.
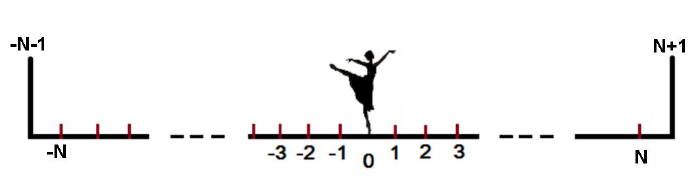
Nu se pot pune obstacole în punctele de coordonate -N - 1, 0 respectiv N + 1. Pereții camerei de coordonate -N - 1 respectiv N + 1 se consideră obstacole permanente ce nu vor dispărea la atingere, iar punctul de coordonată C = 0 reprezintă poziţia iniţială a Costelinei.
Cerintă
Dându-se valorile lui T, N şi K, calculaţi în câte moduri se pot plasa cele K obstacole, astfel încât după o reprezentaţie completă de T paşi Costelina să se întoarcă în punctul de pornire C.
Date de intrare
Fișierul piruete.in conține pe prima linie numerele naturale T, N și K separate prin câte un spaţiu, cu semnificaţiile de mai sus.
Date de ieșire
Fișierul piruete.out va conține pe prima linie un singur număr natural reprezentând răspunsul modulo .
Restricții și precizări
0 ≤ T ≤ 200,Teste număr par ;1 ≤ N ≤ 100;0 ≤ K ≤ 2 * N;- Atentie! Răspunsul se cere modulo ;
- Pentru
10%din teste avemN ≤ 10; - Pentru
30%din teste avemN ≤ 30; - Pentru
70%din teste avemT ≤ 2 * N + 2;
Exemplu:
piruete.in
6 3 4
piruete.out
7
Explicație
Balerina va efectua T = 6 paşi într-o cameră de lungime 2 * N + 2 = 2 * 3 + 2 = 8, se plasează K = 4 obstacole.
Există 7 modalităţi de amplasare a obstacolelor:
[.x.Cxxx]2.[.xxC.xx]3.[x.xC.xx]4.[xx.Cx.x]5.[xx.Cxx.]6.[xxxC.x.]7.[xxxC..x]
S-a notat cu ’ poziţia unui loc liber, respectiv cu x poziţia unui obstacol.