Veri

Se dă un graf orientat cu $n$ noduri și $m$ muchii. Fiecare muchie are costul $1$ (poate fi parcursă într-un minut). Doi „prieteni” (veri) pornesc din nodul $S$. Unul dintre ei vrea să ajungă în nodul $A$, iar celălalt vrea să ajungă în nodul $B$.

Cei doi prieteni se vor plimba împreună până când ciclează, adică până când vor ajunge în același nod a doua oară, notat cu $Z$. După ciclare, ei își pot continua drumurile separat. Totuși, dacă vor, pot să meargă amândoi în continuare pe același drum: doar dispare obligația de a merge împreună.

Fiecare dintre ei trebuie să-și termine drumul doar după ciclare, adică după ce nu mai sunt obligați să meargă împreună. Totuși, este în regulă dacă drumul unuia se termină exact în nodul în care au ciclat (adică ciclează în $A$ sau $B$).

Care este numărul minim de minute necesar astfel încât să fie posibil ca amândoi să ajungă la destinațiile lor, în timpul alocat, în $A$, respectiv $B$?

Cu alte cuvinte, dacă cei doi veri ciclează pentru prima oară după exact $t$ minute, apoi își continuă drumurile pentru alte $t_A$, respectiv $t_B$ minute, vrem să aflăm valoarea minimă a lui $max(t + t_A, t + t_B)$.

Există două tipuri de cerințe, reprezentate printr-un număr $c$:

• Dacă $c = 1$, trebuie calculată valoarea minimă a lui $max(t + t_A, t + t_B)$.
• Dacă $c = 2$, trebuie afișat un triplet de drumuri care poate fi urmat de cei doi veri (drumul comun din $S$ până în $Z$, drum urmat ulterior de primul văr din $Z$ până în $A$, drum urmat ulterior de al doilea văr din $Z$ până în $B$), astfel încât valoarea asociată drumurilor, adică $max(t + t_A, t + t_B)$ să fie minimă. Orice triplet corect cu valoarea asociată minimă poate fi afișat.

Date de intrare

Pe prima linie se găsește $c$. Pe a doua linie se găsesc doi întregi $n$ și $m$. Pe a treia linie se găsesc trei întregi $S$, $A$ și $B$.

Pe următoarele $m$ linii se găsesc câte doi întregi $X$ și $Y$, reprezentând că există o muchie direcționată de la nodul $X$ la nodul $Y$, care poate fi parcursă într-un minut (de cost $1$).

Date de ieșire

Dacă $c = 1$, afișați un singur număr, valoarea minimă a lui $max(t + t_A, t + t_B)$.

Dacă $c = 2$, afișati trei drumuri. Primul drum este format de la $S$ până la $Z$. Al doilea drum este format de la $Z$ până la $A$. Al treilea drum este format de la $Z$ până la $B$, unde $S$, $A$, $B$, $Z$ sunt definite anterior.

Fiecare drum se va tipări pe două linii separate:

• Pe prima linie va apărea lungimea drumului, adică numărul de muchii.
• Pe a doua linie vor apărea nodurile drumului, separate prin câte un spațiu.

Valorea asociată drumurilor, adică $max(t + t_A, t + t_B)$, trebuie să fie minimă.

Restricții și precizări

• $1 \leq S, A, B, Z \leq n \leq 5\ 000$
• Nodurile sunt numerotate de la $1$ la $n$.
• $A \neq B$
• $1 \leq m \leq n \times (n-1)$.
• Se garantează că pentru orice test dat spre rezolvare există cel puțin o soluție.
• Nu există muchii de la un nod la el însuși. Există maxim o muchie orientată între oricare două noduri distincte.
• Dacă verii se despart în $A$, primul văr poate să nu mai facă nimic (drumul lui ulterior ar avea $0$ muchii și l-ar conține doar pe $A$; vezi exemplul 3). Analog pentru $B$.
• Pentru fiecare subtask, testele cu $c = 1$ vor conta pentru $60\%$ din punctaj.
• Pentru 30 de puncte, $n \leq 500$, $m = n$ și toate muchiile sunt de forma $i \rightarrow (i\ mod\ n) + 1$, unde $i \in \{1, ..., n\}$.
• Pentru 50 de puncte, $n \leq 500$.
• Pentru 20 de puncte, $n \leq 5\ 000$ și $m \leq 4 \times n$.

Exemplul 1

veri.in

2
7 8
1 3 4
1 2
2 5
5 7
7 6
6 7
6 5
5 3
7 4

veri.out

5
1 2 5 7 6 5
1
5 3
2
5 7 4

Drumul urmat în comun de cei doi este $1 \rightarrow 2 \rightarrow 5 \rightarrow 7 \rightarrow 6 \rightarrow 5$. Drumul urmat de primul văr în continuare este $5 \rightarrow 3$. Drumul continuat de al doilea văr este $5 \rightarrow 7 \rightarrow 4$. Astfel, primul văr are nevoie de $6$ minute pentru a ajunge în $A$, iar al doilea de $7$ minute pentru a ajunge în $B$, deci răspunsul pentru $c = 1$ este $7$. Cei doi ar fi putut să cicleze în $7$, dacă ar fi urmat drumul $1 \rightarrow 2 \rightarrow 5 \rightarrow 7 \rightarrow 6 \rightarrow 7$. Totuși, deși al doilea văr ar fi ajuns în $B$ în doar $6$ minute ($7 \rightarrow 4$), primul văr ar fi avut nevoie de cel puțin $8$ minute ca să ajungă în $A$ ($7 \rightarrow 6 \rightarrow 5 \rightarrow 3$).

Exemplul 2

veri.in

2
7 8
1 2 5
1 3
1 4
3 2
4 5
6 4
7 3
3 6
4 7

veri.out

5
1 4 7 3 6 4
3
4 7 3 2
1
4 5

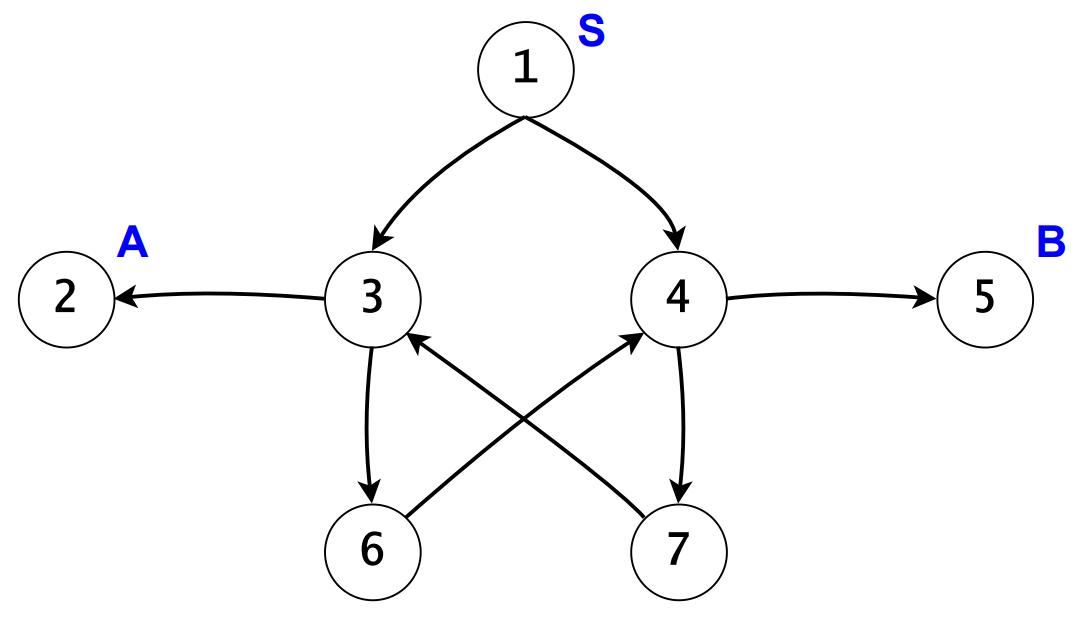
Răspunsul corect pentru $c = 1$ este $8$. Pentru acest exemplu există două soluții corecte. A doua soluție este tripletul de drumuri $(1 \rightarrow 3 \rightarrow 6 \rightarrow 4 \rightarrow 7 \rightarrow 3,\ 3 \rightarrow 2,\ 3 \rightarrow 6 \rightarrow 4 \rightarrow 5)$.

Exemplul 3

veri.in

2
5 6
1 3 5
1 2
2 3
3 4
4 3
3 1
3 5

veri.out

4
1 2 3 4 3
0
3
1
3 5

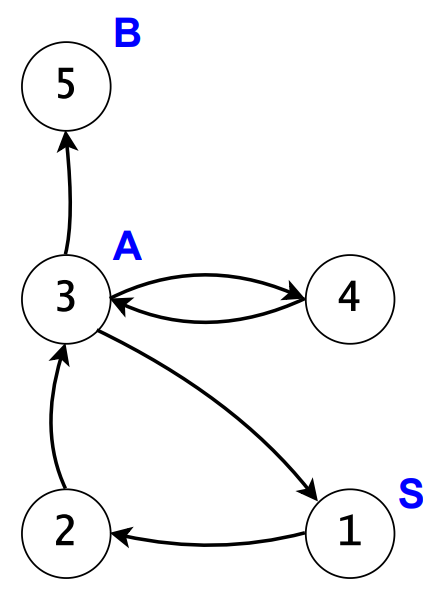
Răspunsul corect pentru $c = 1$ este $5$. Este folosit un ciclu care se termină în $A = 3$.

Exemplul 4

veri.in

1
4 4
1 2 4
1 3
3 2
2 3
2 4

veri.out

5

Pentru $c = 2$, singurul triplet corect de drumuri este $(1 \rightarrow 3 \rightarrow 2 \rightarrow 3,\ 3 \rightarrow 2,\ 3 \rightarrow 2 \rightarrow 4)$.

Atenție! Tripletul $(1 \rightarrow 3 \rightarrow 2 \rightarrow 3 \rightarrow 2,\ 2,\ 2 \rightarrow 4)$ este greșit, deoarece primul nod vizitat a doua oară nu este $2$.