median

Task

You are given a tree with $N$ nodes, numbered from $1$ to $N$. The edges are numbered from $1$ to $N-1$, and edge $i$ has a weight $w_i$.

Consider a simple path connecting two different nodes. If the weights on this path are $w_{i_0} \leq w_{i_1} \leq \dots \leq w_{i_k}$ (not necessarily in this order), then we define its median as $w_{i_{\lfloor k / 2 \rfloor}}$.

Let $M$ be the list of medians of all such simple paths (that is, $|M| = \frac{N (N-1)}{2}$). What is the $K$th smallest element of $M$?

Input

The first line contains two integers, $N$ and $K$ ($1 \le N \le 50 \ 000$), ($1 \le K \le N * (N-1) / 2$). The $i$-th of the following $N-1$ lines contains three integers $u_i$, $v_i$ and $w_i$ ($1 \le u_i, v_i \le N$), ($1 \le w_i \le 10^9$), corresponding to an edge of weight $w_i$ between nodes $u_i$ and $v_i$.

For tests worth $8$ points, $N \le 100$.

For tests worth $19$ more points, $N \le 1 \ 000$.

For tests worth $24$ points, The tree is a bamboo (no node has a degree greater than $2$).

Output

The first and only line must contain a single number: the unique integer that solves this task.

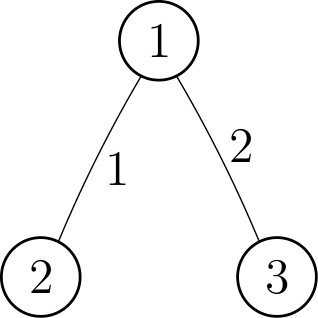
Example 1

stdin

3 3
1 2 1
1 3 2

stdout

2

Example 2

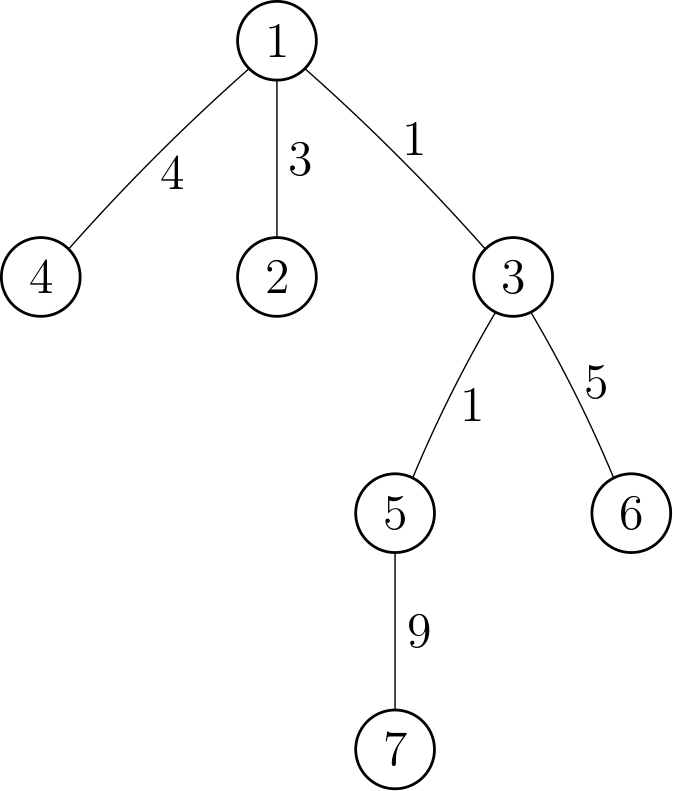
stdin

7 15
1 2 3
1 3 1
1 4 4
3 5 1
3 6 5
5 7 9

stdout

3

Explanation

In the first sample case, the elements of $M$ in increasing order are 1, 1 and 2.

In the second sample case, the elements of $M$ in increasing order are 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 4, 4, 5, 5 and 9.