lrtree

Task

Since spring is coming and thus the tree planting season is about to start as well, Alice and Bob decided to start planning their future adventures.

One day, Bob came with the idea that they could spend their time together planting trees in the magic forest. Since this is a magic forest, the trees they can plant are in fact binary trees!

However, they are not just any kind of binary tree, but rooted binary trees with root at node $1$ and with the property that there are more nodes on the left side of the tree than on the right side of the tree.

This spring they decided that the trees they are going to plant are of size $N$. Since they want to spend as much time as possible in the magic forest, let them know how many distinct binary trees with $N$ nodes exist such that there are more nodes on the left side of the tree than on the right side of the tree.

Since the answer is big, print it modulo $10^9$ + $7$.

A binary tree is a rooted tree with the property that each node has at most two children. Two binary trees are different if they have either a different set of edges or a child is the right child instead of the left child. This means that even though trees can be isomorphic, we will still count each tree as separate.

Input

The first line of the input will contain an even integer $n$, the number of nodes the trees must have ($1 \le n \le 10^6$).

For tests worth $10$ points, ($1 \le n \le 10$).

For tests worth $40$ more points, ($1 \le n \le 2000$).

Output

The output will contain the required answer, modulo $10^9$ + $7$.

Example 1

stdin

4

stdout

7

Explanation

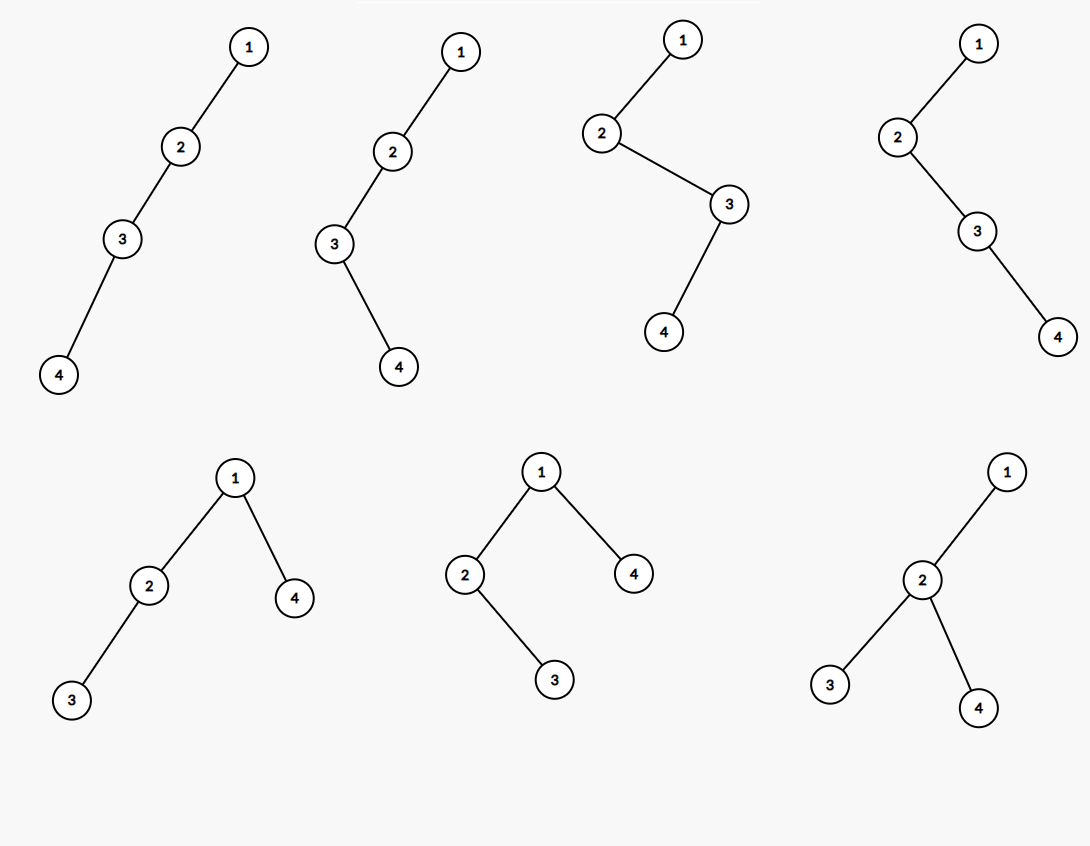
On the image below, the trees we can create with $N$ = $4$ nodes are shown in the drawing. Take note that the condition for the number of nodes from left and right subtrees must be respected only by node $1$ and two trees are also different if we place a vertex on the left or on the right end of a parent subtree, in case the parent has only one adjacent vertex.