Cerință
Keiko Hamada a fost angajată să amenajeze noua grădină Zen a familiei Nomizu. Domnul Nomizu vrea să folosească noua grădină pentru a medita. Din păcate, el nu își poate goli mintea decât dacă grădina respectă o serie de condiții.
Grădina domnului Nomizu trebuie să conțină un singur tip de copac, și anume cireșul. Un cireș poate fi reprezentat ca un arbore cu rădăcină. Definim o creangă a cireșului drept o muchie din reprezentarea sa ca arbore. (În această problemă, tulpina este considerată o creangă.).
În fiecare primăvară, cireșii înfloresc. Ei produc câte o floare în vârful fiecărei crengi care nu se continuă cu nicio altă creangă. Mai exact, florile apar în fiecare nod frunză al reprezentării cireșului ca arbore.
Domnul Nomizu vrea o grădină cu cel mult cireși, așezați pe un singur rând, care să aibă în total crengi. Mai mult, atunci când înfloresc, cireșii trebuie să aibă între și flori. Presupunem că toți cireșii înfloresc în același timp.
Mai formal, o amenajare a grădinii domnului Nomizu este o colecție ordonată de cel mult arbori cu rădăcină cu , cu (aici numărul de muchii ale arborelui ) și cu (aici numărul de frunze ale arborelui ; se numește o frunză a arborelui un nod care nu are copii). Două aranjări și ale grădinii se consideră diferite dacă: sau și există un indice cu proprietatea că arborii și nu sunt identici.
Fie și doi arbori cu rădăcină. Dacă , atunci spunem că și sunt identici. Dacă și considerăm și listele ordonate de copii ale rădăcinii arborelui și respectiv . și sunt identici dacă și identic cu identic cu identic cu (aici am notat cu subarborele cu rădăcina în nodul ). În rest, spunem că și nu sunt identici.
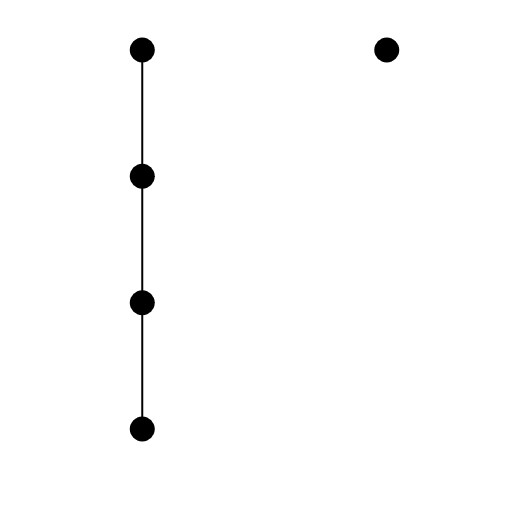
În figura de mai jos, conform definiției, cei doi arbori sunt identici.
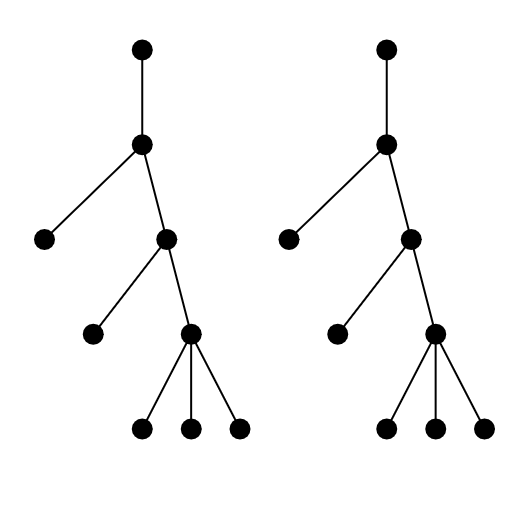
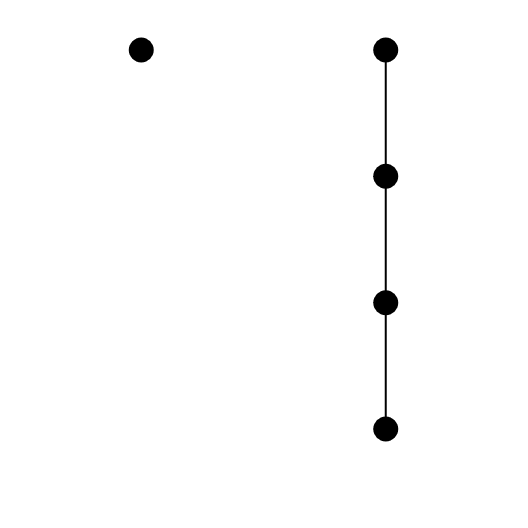
În figura de mai jos, conform definiției, cei doi arbori nu sunt identici.
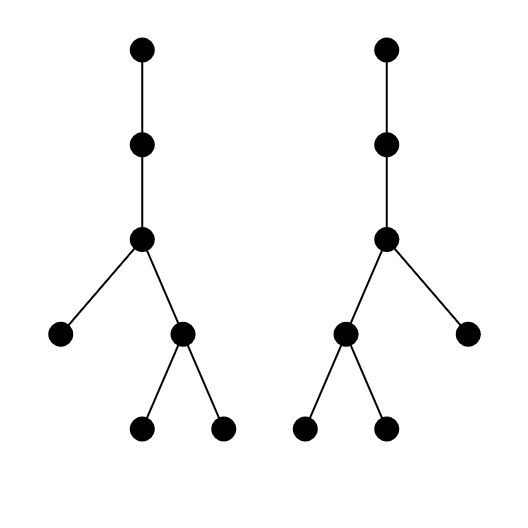
Keiko vă întreabă în câte moduri ar putea planta cireșii domnului Nomizu, astfel încât să-i satisfacă pretențiile. Pentru că acest număr poate fi foarte mare, Keiko se va mulțumi cu valoarea sa modulo .
Date de intrare
Pe prima linie se găsesc numerele în această ordine cu semnificația din enunț.
Date de ieșire
Pe prima linie se va afișa un singur număr natural, reprezentând numărul de moduri în care Keiko îi poate aranja grădina domnului Nomizu (modulo ).
Restricții și precizări
- Pentru teste în valoare de puncte,
- Pentru teste în valoare de alte puncte,
- Pentru teste în valoare de alte puncte,
Exemplul 1
stdin
1 3 1 2
stdout
4
Explicație
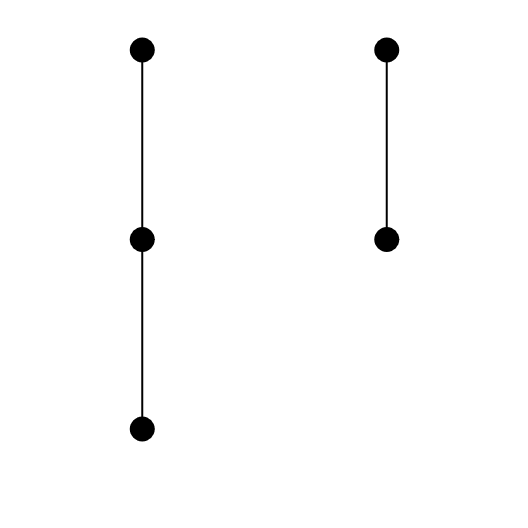
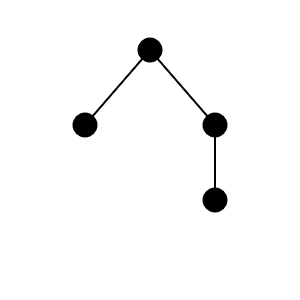
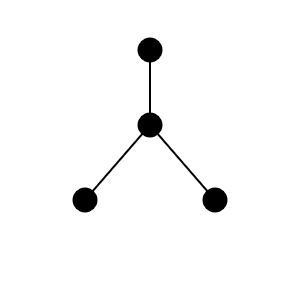
Cele 4 moduri în care Keiko poate amenaja grădina sunt următoarele:
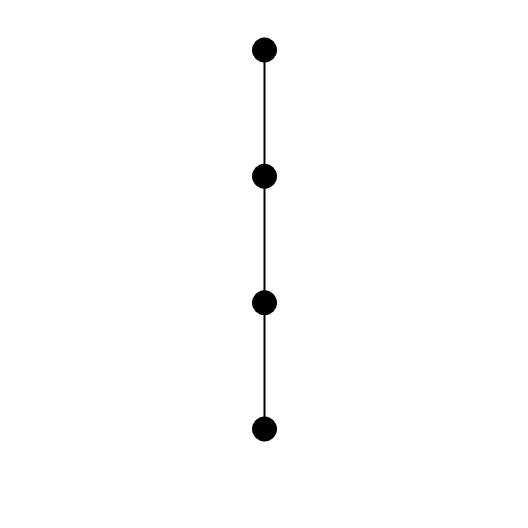
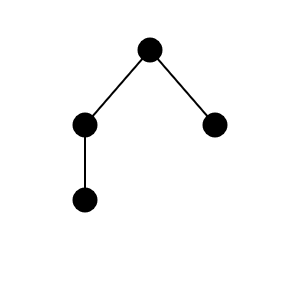
Exemplul 2
stdin
2 3 2 2
stdout
7
Explicație
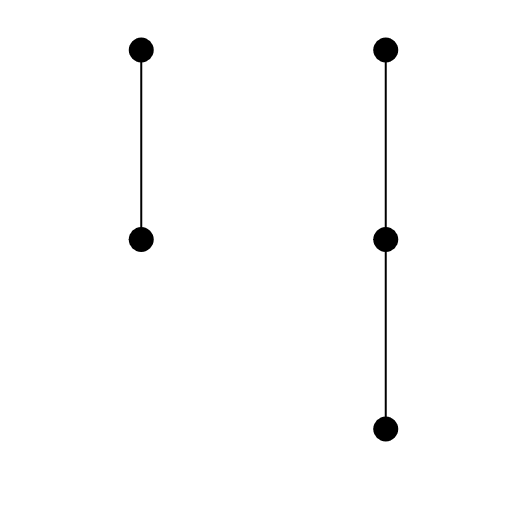
Cele 7 moduri în care Keiko poate amenaja grădina sunt următoarele: