Casă

Nu am nicio glumă la problema asta.

Cerință

Mihăiță se joacă un joc cu sora sa mai mare. Acesta constă într-o tablă cu $N$ linii și $M$ coloane. Inițial, tabla este goală. Sora sa face $Q$ mișcări pe tabla de joc. Fiecare mișcare poate fi de tipul $1$ sau $2$:

• 1 i j - Mișcare de tipul 1. Sora sa plantează un copac pe poziția $(i, j)$.
• 2 i j - Mișcare de tipul 2. Sora sa îi pune următoarea întrebare lui Mihăiță: „Care este cea mai mare casă pe care o poți construi pe tablă și care conține celula $(i, j)$ în interiorul ei, dacă luăm în considerare copacii plantați până acum?”.

Casele au formă dreptunghiulară, cu laturile paralele cu marginile tablei de joc. O casă poate fi identificată prin colțul stânga-sus $(i_1, j_1)$ și colțul dreapta-jos $(i_2, j_2)$. O casă poate fi construită într-o locație dacă:

• Nu se află niciun copac în interiorul acesteia.
• Din fiecare poziție din aceasta, putem vedea toate marginile tablei fără a fi blocați de vreun copac în oricare direcție.

Formal, o casă $(i_1, j_1)$ $(i_2, j_2)$ poate fi construită dacă nu există niciun copac $(i_c, j_c)$ (plantat până la momentul întrebării) care să îndeplinească $i_1 \leq i_c \leq i_2$ sau $j_1 \leq j_c \leq j_2$. Mărimea unei case este aria dreptunghiului.

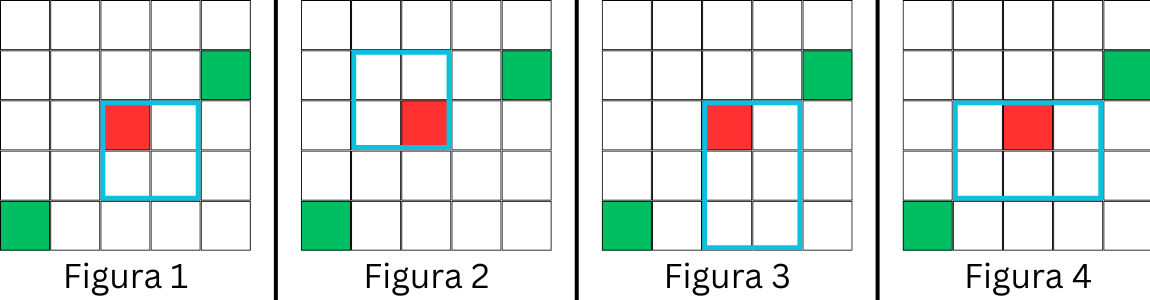
În figurile $1-4$, vedem o tablă cu $5$ linii și $5$ coloane. Sora lui Mihăiță a plantat $2$ copaci pe pozițiile $(2, 5)$ și $(5, 1)$. Acum, ea îi pune o întrebare (mișcare de tipul $2$) pe poziția $(3, 3)$.

• În figura 1, casa $(3, 3)$ $(4, 4)$ este construită corect.
• În figura 2, casa $(2, 2)$ $(3, 3)$ nu este construită corect, deoarece copacul $(2, 5)$ blochează vederea spre marginea dreaptă a tablei.
• În figura 3, casa $(3, 3)$ $(5, 4)$ nu este construită corect, deoarece copacul $(5, 1)$ blochează vederea spre marginea stângă a tablei.
• În figura 4, casa $(3, 2)$ $(4, 4)$ este construită corect. Aceasta este cea mai mare casă care poate fi construită între cei $2$ copaci, cu aria $6$.

Mihăiță s-a plictisit rapid de acest joc, așa că este rândul vostru să vă jucați împotriva surorii lui.

Date de intrare

Pe prima linie a fișierului de intrare casa.in se găsesc $3$ numere întregi, $N$, $M$ și $Q$, reprezentând dimensiunile tablei și numărul de mișcări ale fetei.
Pe fiecare din următoarele $Q$ linii, se găsesc $3$ numere întregi, $c$, $i$, $j$, care descriu o mișcare din cele $2$ tipuri posibile ($c = 1$ sau $c = 2$).

Date de ieșire

Pentru fiecare operație de tipul $2$, se va afișa în fișierul de ieșire casa.out, pe câte o linie, aria maximă a unei case care respectă condițiile (în ordinea mișcărilor de tipul $2$ din fișierul de intrare).

Restricții și precizări

• $1 \leq N, M \leq 10^9$;
• $1 \leq Q \leq 100 \ 000$;
• $1 \leq i_k \leq N$ și $1 \leq j_k \leq M$, pentru $1 \leq k \leq Q$;
• Copacii plantați au poziții diferite;
• Dacă $c = 2$ (mișcare de tipul $2$), atunci nu va exista niciun copac $(i_c, j_c)$ cu $i_c = i$ sau $j_c = j$ (aria maximă a casei cerute nu va fi niciodată $0$);

Exemplu

casa.in

4 5 5
1 2 4
2 3 2
1 4 1
2 3 3
2 1 5

casa.out

6 
2 
1

Explicație

Pentru prima întrebare, singurul copac plantat este $(2, 4)$. Cea mai mare casă pe care o putem construi este $(3, 1)$ $(4, 3)$ cu aria $6$. Pentru a doua și a treia întrebare, casele optime sunt $(3, 2)$ $(3, 3)$, respectiv $(1, 5)$ $(1, 5)$.