xnsgraph

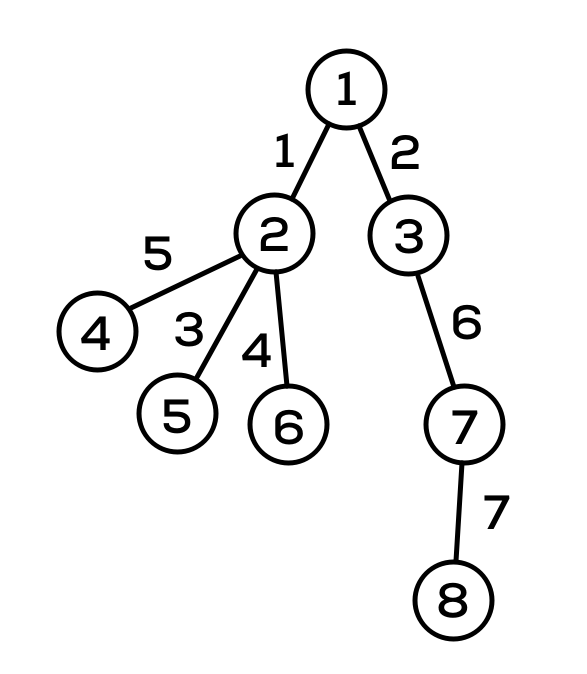
Given a tree with $N$ nodes, numbered from $1$ to $N$. A partial graph $G'(V, E')$ of the graph $G(V, E)$ is the graph obtained using a subset of edges $E'$ such that $E' \subseteq E$.

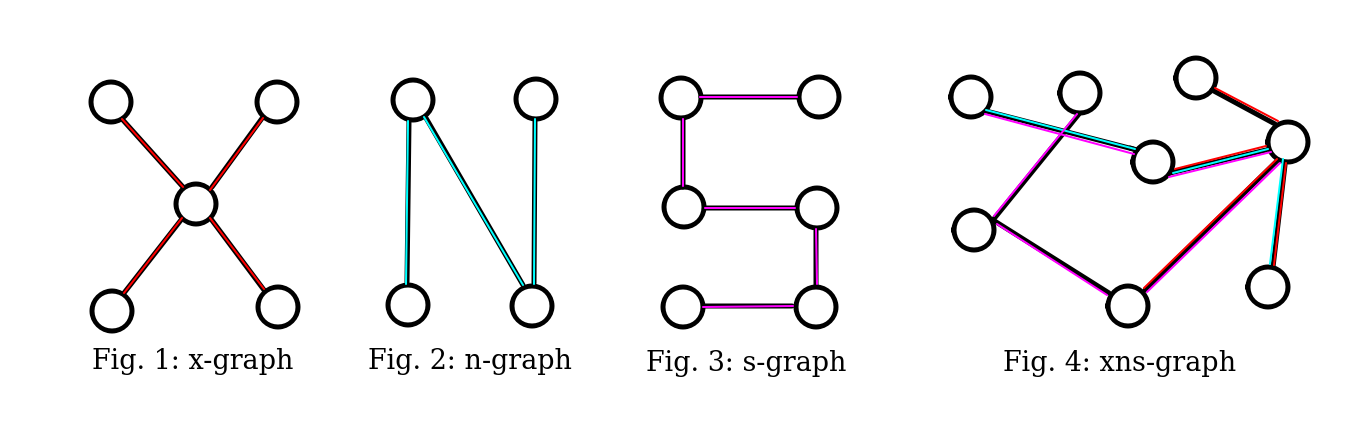
A graph is an $x$-graph if there exists an "x", or if $\exists K \in V$ such that $deg(K) \geq 4$.

A graph is an $n$-graph if there exists an "n", or if there exists a simple path of at least $4$ nodes.

A graph is an $s$-graph if there exists an "s", or if there exists a simple path of at least $6$ nodes.

A graph is an $xns$-graph if it satisfies all the conditions above.

Task

You are given $Q$ queries of the form $[l, r]$, asking whether the partial graph of the tree formed by the edges in the interval $[l, r]$ is an $xns$-graph.

Input data

The first line will contain two integers, $N$ and $Q$, as described above.

Each of the next $N-1$ lines will contain a pair of positive integers $a_i$ and $b_i$, separated by spaces, representing edge $i$.

Each of the next $Q$ lines will contain a pair of positive integers $l_i$ and $r_i$, separated by spaces, representing the $i$-th query.

Output data

Line $i$ should contain the answer corresponding to the $i$-th query from the input.

Constraints and clarifications

• $1 \leq N, Q \leq 100 \ 000$;
• $1 \leq a_i, b_i \leq N$;
• $1 \leq l_i \leq r_i \leq N-1$;
• $deg(K)$ denotes the degree of the node $K$ in the graph;
• A simple path is a path in which no nodes or edges can appear more than once.
• The $x$, $n$, and $s$ can overlap, i.e., they do not have to be disjoint;
• Due to the very large input set, it is recommended to use fastio.
• For tests worth $10$ points: $N, Q \leq 100$;
• For other tests worth $20$ points: $N, Q \leq 2 \ 000$;
• For other tests worth $20$ points: $l_i = 1$ for all queries;
• For other tests worth $19$ points: $N, Q \leq 60 \ 000$;
• For other tests worth $31$ points: no additional constraints.

Example 1

stdin

8 7
1 2
1 3
2 5
2 6
2 4
3 7
7 8
1 1
1 2
1 3
1 4
1 5
1 6
1 7

stdout

0
0
0
0
0
0
1

Explanation

Below you can find the graphical representation of the given tree, where the labels of the edges represent their index (input order).