Mușuroi

Un mușuroi format din mai multe celule este reprezentat ca o matrice cu $N$ linii, numerotate de la 1 la $N$, și $M$ coloane, numerotate de la 1 la $M$, fiecare element al matricii corespunzând unei celule. Poziţia unei celule din mușuroi este identificată prin linia şi coloana pe care se află. În fiecare celulă a mușuroiului este desenată o săgeată, care indică sensul în care o furnică aflată în poziţia respectivă se va deplasa. Săgețile sunt codificate cu numere de la $0$ la $7$.

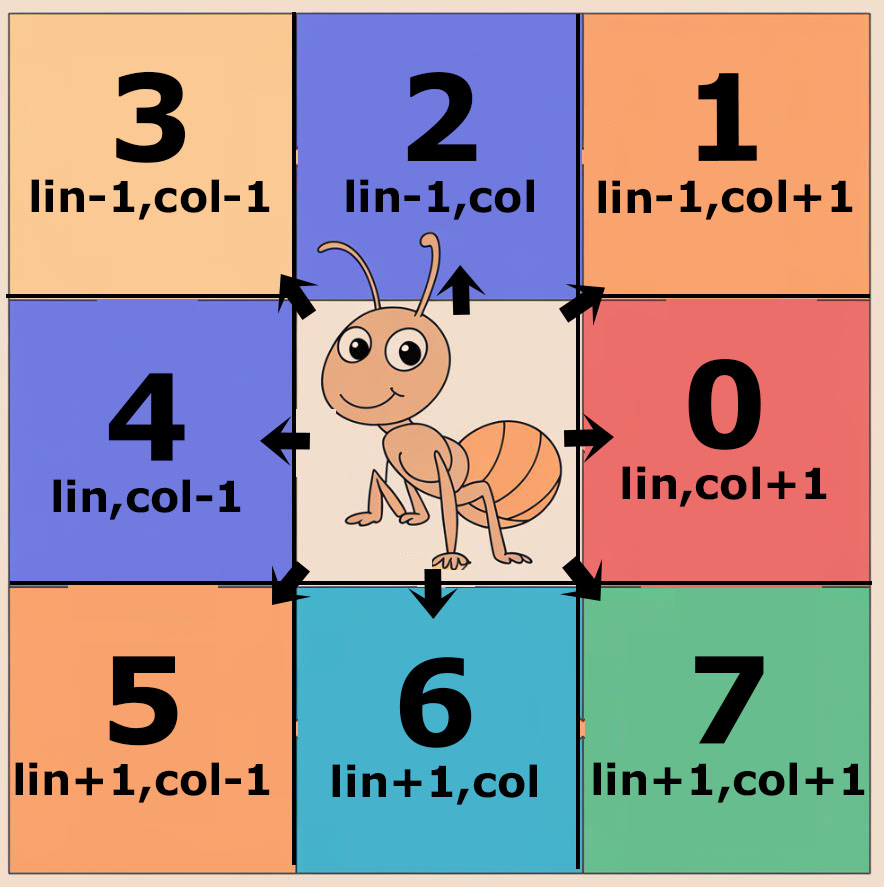
Dacă furnica se află în celula ($lin$, $col$) la momentul $t$, atunci la momentul $t+1$ ea va ajunge în poziţia:

• ($lin$, $col+1$), dacă săgeata este 0;
• ($lin-1$, $col+1$), dacă săgeata este 1;
• ($lin-1$, $col$), dacă săgeata este 2;
• ($lin-1$, $col-1$), dacă săgeata este 3;
• ($lin$, $col-1$), dacă săgeata este 4;
• ($lin+1$, $col-1$), dacă săgeata este 5;
• ($lin+1$, $col$), dacă săgeata este 6;
• ($lin+1$, $col+1$), dacă săgeata este 7.

În figura alăturată sunt ilustrate săgeţile, fiind indicată poziţia în care ajunge furnica pentru fiecare dintre ele.

Cerință

Cunoscând reprezentarea muşuroiului, scrieţi un program care să răspundă la $Q$ întrebări de forma $lin_A$ $col_A$ $lin_B$ c$ol_B$ $K$, cu semnificația “Dacă o furnică pornește de la celula ($lin_A$, $col_A$) la momentul de timp $t=0$, la ce moment de timp va ajunge a $K$-a oară în poziţia ($lin_B$, $col_B$)?”. Se garantează că furnica poate trece de cel puțin $K$ ori prin celula ($lin_B$, $col_B$) dacă pornește din celula ($lin_A$, $col_A$).

Date de intrare

Fișierul de intrare musuroi.in conţine pe prima linie numerele naturale $N$ și $M$ cu semnificația din enunț. Pe următoarele $N$ linii se află câte $M$ numere cuprinse între 0 și 7, ce reprezintă săgețile din fiecare celulă a matricii. Pe linia $N+2$ se află numărul natural $Q$, reprezentând numărul de întrebări, iar pe următoarele $Q$ linii se află cele $Q$ întrebări, câte o întrebare pe o linie, în forma descrisă mai sus. Valorile scrise pe aceeaşi linie sunt separate prin câte un spaţiu.

Date de ieșire

Fișierul de ieșire musuroi.out conține $Q$ linii, pe linia $i$ aflându-se un număr ce reprezintă răspunsul pentru cea de a $i$-a întrebare din fişierul de intrare ($1 \leq i \leq Q$).

Restricții și precizări

• $2 \leq N, M \leq 1 \ 000$
• $1 \leq Q \leq 100 \ 000$
• În întrebările pentru care $K=1$ poziţiile ($lin_A$, $col_A$) şi ($lin_B$, $col_B$) pot să coincidă, caz în care răspunsul este 0.
• $1 \leq K \leq 1 \ 000 \ 000 \ 000$
• Se garantează că furnica, deplasându-se în sensul săgeţilor, va rămâne în muşuroi.

Exemplul 1

musuroi.in

6 6
7 6 4 0 0 6
0 5 2 0 3 4
2 5 0 5 2 6
0 7 5 0 6 3
6 1 7 2 0 6
0 0 0 0 2 4
2
2 4 2 6 1
4 2 6 6 1

musuroi.out

5
6

Explicație

Prima întrebare: furnica pleacă la momentul $t=0$ din poziţia $(2,4)$. Traseul furnicii este:
$(2,4) \rightarrow (2,5) \rightarrow (1,4) \rightarrow (1,5) \rightarrow (1,6) \rightarrow (2,6)$. La momentul $t=5$ a ajuns la destinaţie, în poziţia $(2,6)$ pentru prima dată ($K=1$).

A doua întrebare: furnica pleacă la momentul $t=0$ din poziţia $(4,2)$. Traseul furnicii este:
$(4,2) \rightarrow (5,3) \rightarrow (6,4) \rightarrow (6,5) \rightarrow (5,5) \rightarrow (5,6) \rightarrow (6,6)$. La momentul $t=6$ a ajuns la destinaţie, în poziţia $(6,6)$ pentru prima dată ($K=1$).

Exemplul 2

musuroi.in

6 6
7 6 4 0 0 6
0 5 2 0 3 4
2 5 0 5 2 6
0 7 5 0 6 3
6 1 7 2 0 6
0 0 0 0 2 4
2
2 4 2 6 3
4 2 6 6 5

musuroi.out

15
22

Explicație

Prima întrebare: furnica pleacă la momentul $t=0$ din poziţia $(2,4)$. Traseul furnicii este:
$(2,4) \rightarrow (2,5) \rightarrow (1,4) \rightarrow (1,5) \rightarrow (1,6) \rightarrow (2,6) \rightarrow (2,5) \rightarrow (1,4) \rightarrow (1,5) \rightarrow (1,6) \rightarrow (2,6) \rightarrow (2,5) \rightarrow (1,4) \rightarrow (1,5) \rightarrow (1,6) \rightarrow (2,6)$. La momentul $t=15$ a ajuns la destinaţie, în poziţia $(2,6)$ pentru a treia oară ($K=3$).

A doua întrebare: furnica pleacă la momentul $t=0$ din poziţia $(4,2)$. Traseul furnicii este:
$(4,2) \rightarrow (5,3) \rightarrow (6,4) \rightarrow (6,5) \rightarrow (5,5) \rightarrow (5,6) \rightarrow (6,6) \rightarrow (6,5) \rightarrow (5,5) \rightarrow (5,6) \rightarrow (6,6) \rightarrow (6,5) \rightarrow (5,5) \rightarrow (5,6) \rightarrow (6,6) \rightarrow (6,5) \rightarrow (5,5) \rightarrow (5,6) \rightarrow (6,6) \rightarrow (6,5) \rightarrow (5,5) \rightarrow (5,6) \rightarrow (6,6)$. La momentul $t=22$ a ajuns la destinaţie, în poziţia $(6,6)$ pentru a cincea oară ($K=5$).