notdivisible

Task

You have a tree (a connected acyclic graph) of $N$ nodes indexed from $1$ to $N$. Each node $i$ has an integer value $V_i > 1$ assigned to it.

You are given $Q$ queries, where each query $i$ consists of two integers $A_i$ and $B_i$. Your task is to find the minimum value (greater than 1) that is not divisible by any of the assigned values on the path between $A_i$ and $B_i$, including the values assigned to $A_i$ and $B_i$.

Input

The first line contains one integer $N$ ($2 \le N \le 100\ 000$), the number of nodes. The second line contains $N$ integers $V_1, V_2, \ldots, V_N$ ($2 \le V_i \le 100\ 000\ 000$).

Each of the following $N-1$ lines contains two integers $a$ and $b$, meaning that there is an edge between $a$ and $b$.

The next line contains one integer $Q$ ($1 \le Q \le 100\ 000$), the number of queries. Each of the next $Q$ lines contains two integers $A_i$ and $B_i$, describing a query.

For tests worth $5$ points: $N, Q \le 1000$ and every node is connected to at most $2$ other nodes.

For tests worth $5$ points: $N, Q \le 1000$.

For tests worth $10$ points: $V_i \le 3$ for each $i=1\ldots N$ and every node is connected to at most $2$ other nodes.

For tests worth $10$ points: $V_i \le 3$ for each $i=1\ldots N$.

For tests worth $10$ points: All $V_i$ values are unique for $i=1\ldots N$ and every node is connected to at most $2$ other nodes.

For tests worth $15$ points: All $V_i$ values are unique for $i=1\ldots N$.

For tests worth $20$ points: Every node is connected to at most $2$ other nodes.

For tests worth $25$ points: No additional limitations.

Output

For each query, you need to write a single line with an integer representing the answer to that query.

stdin

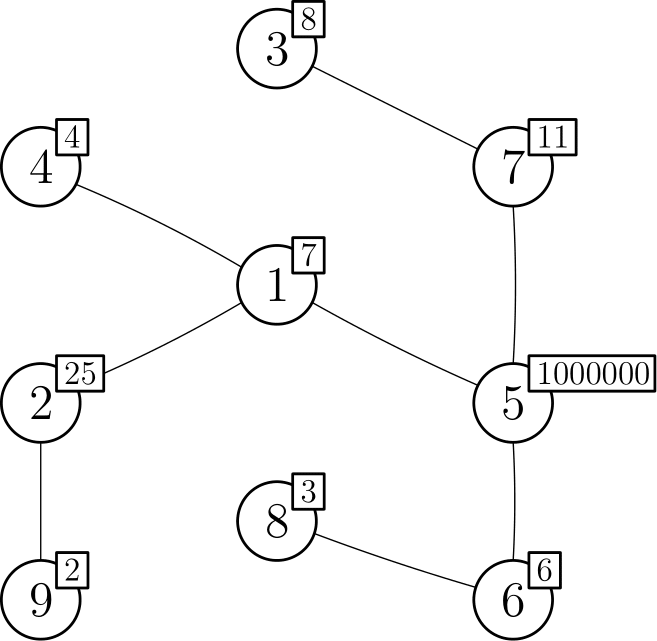
9
7 25 8 4 1000000 6 11 3 2
5 7
5 1
5 6
7 3
1 2
1 4
6 8
2 9
3
8 9
3 8
4 9

stdout

5
2
3

Notes

In the sample case:

• Node values on the path of the first query are $3$, $6$, $1000000$, $7$, $25$, $2$. The minimum integer not divisible by any of them is $5$.
• Node values on the path of the second query are $8$, $11$, $1000000$, $6$, $3$. The minimum integer not divisible by any of them is $2$.
• Node values on the path of the third query are $4$, $7$, $25$, $2$. The minimum integer not divisible by any of them is $3$.