magicforest

Task

In a magical forest far-far away lives the Miraculous Deer. It likes to take magical walks along the trails of the forest. You're wondering, how many distinct magical walks could it take?

The forest contains $N$ trees and there are $M$ trails connecting tree $a_i$ and $b_i$ with a magical value of $c_i$. A walk starts at a tree and goes through a number of trails arriving at a tree. It might visit the same tree multiple times. The length of the walk is the number of trails it uses. A walk of length $k$ is said to be a magical walks if the magical values of the trails it visits in order are $m_1, m_2, \ldots, m_k$ and:

• $k \geq 1$,
• $m_i+1=m_{i+1}$ for all $1 \leq i \leq k-1$.

Two magical walks are different if the set of their trails are different.

Write a program that calculates number of different magical walks modulo $10^9+7$!

Input

The first line contains the integers $N$ ($2 \le N \le 500\ 000$) and $M$ ($1 \le M \le \min\left( \frac{N(N-1)}{2}, 1\ 000\ 000 \right)$).

The following $M$ lines contains three integers $a_i$, $b_i$ and $c_i$ ($1 \le a_i \neq b_i \leq N$ for each trail; $1 \le c_i \leq 10^9$ for each trail) representing a trail between trees $a_i$ and $b_i$ with a magical value of $c_i$.

Any pair of meadows is connected by at most one trail.

For tests worth $7$ points: $a_i=i$ and $b_i=i+1$ for all trails and $M=N-1$.

For tests worth $9$ points: $c_i \leq 3$ for all trails.

For tests worth $14$ points: $N \le 22$ and $M \leq 22$.

For tests worth $20$ points: $N \le 1000$ and $M \le 5000$.

For tests worth $50$ points: No additional limitations.

Output

You need to write a single line with an integer: the number of magical walks modulo $10^9+7$.

stdin

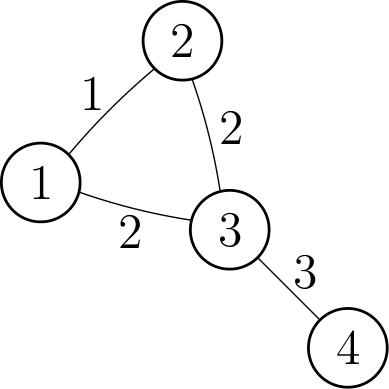
4 4
1 2 1
2 3 2
3 4 3
1 3 2

stdout

10

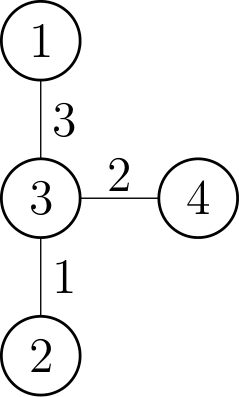
stdin

4 3
1 3 3
3 4 2
3 2 1

stdout

5

stdin

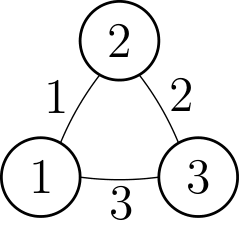
3 3
1 2 1
2 3 2
3 1 3

stdout

6

Notes

In the first sample case the $10$ magical walks are:

• length of $1$: $1 - 2$, $2 - 3$, $3 - 1$, $3 - 4$,
• length of $2$: $1 - 2 - 3$, $2 - 1 - 3$, $2 - 3 - 4$, $1 -3 - 4$,
• length of $3$: $1 - 2 - 3 - 4$, $2 - 1 - 3 - 4$.

In the second sample case there are $3$ magical walks of length $1$, and $2$ of length $2$.

In the third sample case there are $3$ magical walks of length $1$, and $2$ of length $2$ and $1$ of length $3$.