
Task
Because time means money, and students don't have either, much like CFR Cluj's trophy cabinet, this problem will not have a story:
You have to process queries of the following types:
1 x y: Activate point . It is guaranteed that an already active point with the same or coordinate does not exist.2 x y: Deactivate point . It is guaranteed that point is active at the moment.3 x y: Draw open line segments ( segments which do not contain their endpoints) from point , which is active at the moment, to all the other active points, and then print the maximum total number of intersections of a "plus" with these drawn segments (if more than one intersection occurs at the same point, all of them are counted separately). A "plus" centered in , where , is a shape formed from the two lines with equations and .
Observation: The open line segments drawn in queries of type are deleted after printing the answer (i.e. they do not persist through queries).
Input data
The first line contains an integer, the number of queries .
The next lines will each contain three integers , and - the parameters of the queries.
Output data
For each query of type , print the maximum number of intersections of a "plus" with the drawn open line segments.
Constraints and clarifications
- It is guaranteed that there is at least one query of type .
- It is guaranteed that for queries of type , there does not exist any active point with the same or coordinate.
- It is guaranteed that for queries of type and , the point is active.
| # | Points | Restrictions |
|---|---|---|
| 1 | 24 | |
| 2 | 40 | Queries of type do not exist, all the queries with type appear before all the queries of type |
| 3 | 36 | No additional restrictions |
Example 1
stdin
17
1 0 0
1 1 1
1 -1 -1
3 0 0
1 -2 3
1 3 -2
3 0 0
3 -1 -1
2 0 0
1 4 4
3 1 1
2 1 1
1 2 2
3 4 4
3 2 2
3 -2 3
3 3 -2
stdout
2
4
6
4
8
4
7
7
Explanation
Down below there is a graphic for the first example and query , illustrating the intersections:
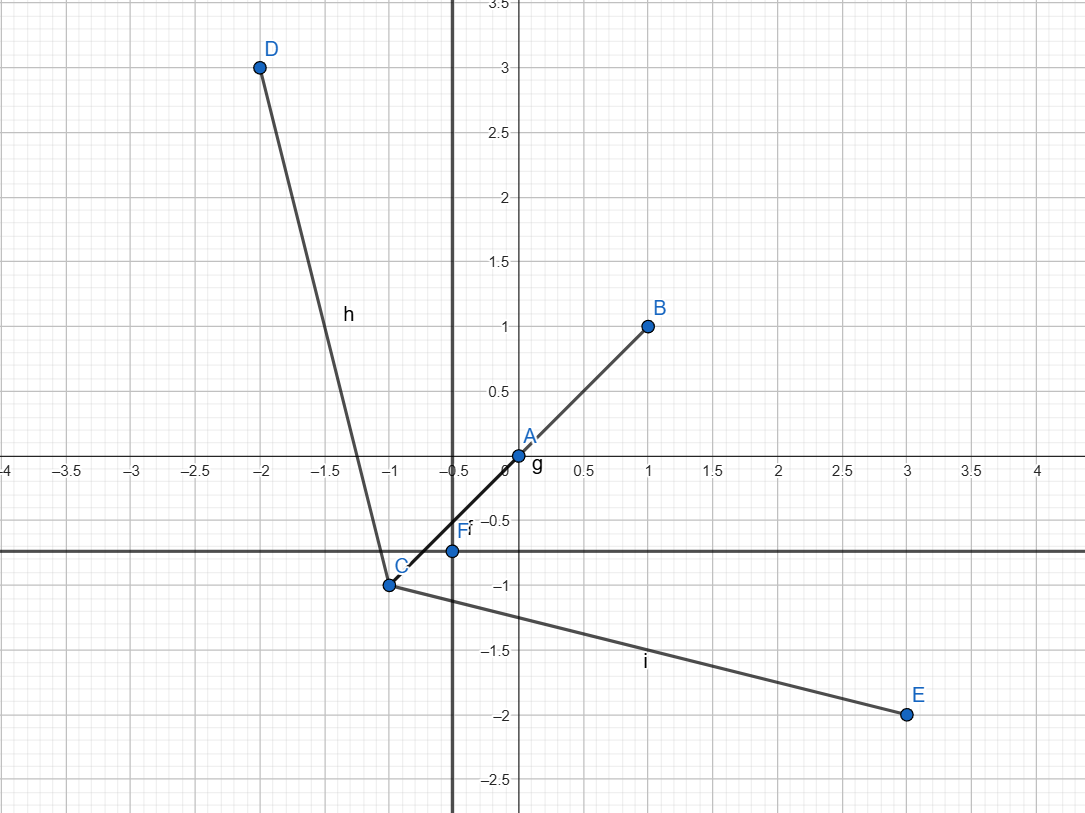
The active points are: , , , , .
A "plus" centered in point has intersections, since:
- Its vertical line intersects the segments , and .
- Its horizontal line intersects the segments , and .
Example 2
stdin
4
1 905580697 285643736
2 905580697 285643736
1 687880848 -231766091
3 687880848 -231766091
stdout
0
Example 3
stdin
13
1 0 0
1 1 1
1 -1 -1
1 -2 3
1 3 -2
1 4 4
1 2 2
3 -1 -1
3 1 1
3 4 4
3 2 2
3 -2 3
3 3 -2
stdout
10
6
12
8
11
11