
Task
In the stands of a match played by Universitatea Craiova, there are groups of supporters arranged in a linear manner, where each group () initially consists of people.
A brawl between two adjacent groups of sizes and respectively will have the following consequences:
- If , then the first group will remain with people, the second group will have people left, and the remaining people from the first group will occupy the section of the stands previously occupied by the second group.
- If , then the second group will remain with people, the first group will have people left, and the remaining people from the second group will occupy the section of the stands previously occupied by the first group.
- If , then both groups will leave (by mutual agreement) from the stadium, and the regions in the stands where these two groups were will be occupied by the neighboring groups (if they exist).
Starting from the initial state, how many groups can remain alone in the stands after a series of brawls?
Input data
Each test contains multiple test cases. The first line will contain the number of test cases .
Each test case contains a single number - the number of groups in the stands.
Output data
For each test case, print the number of groups that can remain alone in the stands after a series of brawls, starting from the initial state.
Constraints and clarifications
- .
- .
| # | Score | Restrictions |
|---|---|---|
| 1 | 17 | |
| 2 | 18 | |
| 3 | 26 | |
| 4 | 28 | |
| 5 | 11 | No additional restrictions |
Example
stdin
5
4
5
8
11
12
stdout
1
3
4
7
8
Explanation
In the first test case, there are groups, with sizes , , , and people respectively.
The only group that can remain alone in the stadium is group , after the following series of brawls:

The above image pictures a series of brawls after which group remains alone in the stadium.
The numbers inside the cells represent the sizes of the groups, and the numbers above the cells represent the group controlling the respective region in the stands.
In the second test case, the groups that can remain alone in the stadium are , , and .
A series of brawls after which group is the only one left is described below:
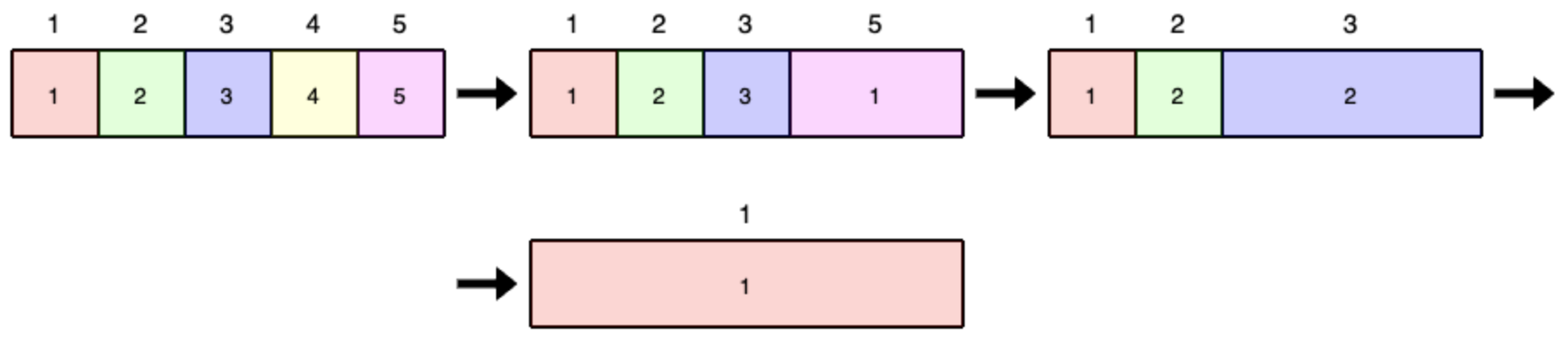
A series of brawls after which group remains alone in the stadium. In the last brawl, groups and have the same number of people, so they leave the stands by mutual agreement. The regions in the stands where groups and were are occupied by group .
In the third test case, the groups that can remain alone in the stadium are , , , and .
In the fourth test case, the groups that can remain alone in the stadium are , , , , , , and .
In the fifth test case, the groups that can remain alone in the stadium are , , , , , , , and .