Task
You are given a tree with nodes. Each edge has a weight . The difference of two nodes and is the binary XOR of the weights on the simple path that connects them. More formally, if the simple path between and consists of the edges , then their difference is defined as .
Let be the set of interesting nodes ( is initially empty). You have to perform operations on this set: in one operation, a node is either added or removed from . After each operation, you have to print the maximum difference between two distinct interesting nodes (if , you must print ).
Input
The first line contains two integers, () and (). The -th of the following lines contains three integers , ( for each .) and ( for each ), corresponding to an edge of weight between nodes and .
Each of the next lines contains a single integer ( for each ). If , then node gets added to , otherwise it gets deleted from .
For tests worth : .
For tests worth : for each .
For tests worth : .
For tests worth : No additional limitations.
Output
You need to print lines. The -th line must contain a single integer, the maximum difference between two interesting nodes after the -th operation.
stdin
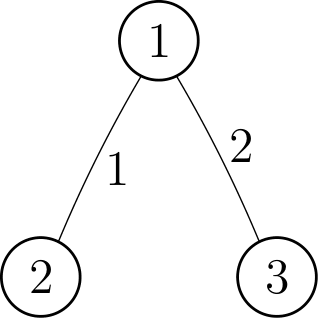
3 4
1 2 1
1 3 2
1
2
3
2
stdout
0
1
3
2
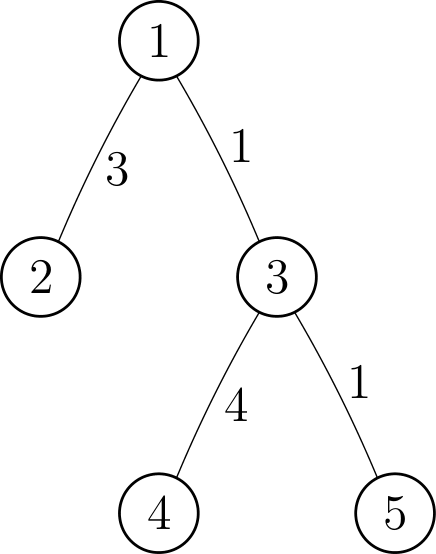
stdin
5 5
1 2 3
1 3 1
3 4 4
3 5 1
3
1
4
3
2
stdout
0
1
5
5
6
Notes
In the first sample case, the set of interesting nodes and the interesting pair with the maximum difference after each operation:
| No. of operation | Set of interesting nodes | Pair with maximum difference |
|---|---|---|
| 1 | No pairs | |
| 2 | ||
| 3 | ||
| 4 |
In the second sample case, the set of interesting nodes and the interesting pair with the maximum difference after each operation:
| No. of operation | Set of interesting nodes | Pair with maximum difference |
|---|---|---|
| 1 | No pairs | |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 |