Task
Little Square has started jumping on trampolines from his school’s gym. In the gym there are trampolines arranged in a rectangular grid with rows and columns. Each trampoline is either green or blue. There are exactly green trampolines. Let denote the trampoline in the row and column. We index the rows from to and the columns from to .
Little Square’s teacher has asked him to practice T gymnastics routines. The ith routine has the following
rules:
- The routine starts at trampoline .
- The routine ends at trampoline .
- If Little Square jumps on a green trampoline at position then he may go to trampolines or , as long as these are not outside the grid.
- If Little Square jumps on a blue trampoline at position then he may go to trampoline , as long as it is not outside the grid.
Little Square wants to know, for each routine, if it is possible to accomplish his teacher’s request.
Input data
On the first line of the input you will find , and . On the next lines you will find the positions of the green trampolines. If a line contains integers then there is a green trampoline at position . On the next line you will find . On the next lines you will find the descriptions of the gymnastics routines. On the of these lines you will find .
Output data
Output lines. The line should contain Yes if it possible to accomplish the routine, and No if it
is not.
Constraints and clarifications
- The coordinates of green trampolines are pairwise distinct.
| # | Points | Restrictions |
|---|---|---|
| 1 | 23 | |
| 2 | 20 | |
| 3 | 11 | |
| 4 | 19 | |
| 5 | 27 | No additional constraints. |
Example
stdin
4 5 2
2 2
3 4
3
2 1 4 5
1 2 1 4
2 3 4 4
stdout
Yes
Yes
No
Explanation
The trampolines are placed like so:
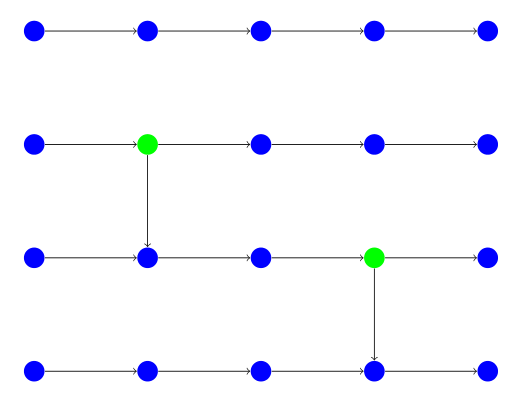
In the first routine Little Square can go on the following route: .
In the second routine Little Square can go on the following route: .
The third routine cannot be accomplished.
No route exists from to that respects Little Square’s teacher’s rules.