Cerință
Seara a poposit deasupra satului în care se află elevul Vasile, deci nu se mai poate juca cu furnicile. El se întoarce înapoi în casă în căutare de noi joculețe în absența internetului. În interior, pe masa din camera de zi, se odihnea lanterna cea de încredere a bunicilor, care conform spuselor bunicilor lui, ”luminează și stelele”.
Vasile s-a dus afară pentru a număra stelele de pe cer cu ajutorul lanternei sale, dar cu un ”twist” micuț. El nu poate vedea decât stelele care sunt luminate de către lanterna sa. Din cauza faptului că nu sunt lumini la el la țară, raza de lumina a lanternei se vede de parcă ar atinge stelele.
Cerul este populat de stele, fiecare cu o poziție în spațiu definită de coordonatele . Vasile se află în curtea sa acum, într-o poziție fixă considerată de coordonate . El îndreaptă lanterna pe care o folosește către un punct de coordonate , și se întreabă câte din stelele de pe cer sunt vizibile cu ajutorul lanternei.
Deoarece bunicii lui Vasile au observat că se distra în timp ce se juca, au decis să îi aducă mai multe lanterne, pe care el le va folosi, având acum un total de lanterne diferite.
Fiecare lanternă are un unghi de vizibilitate sub forma unui con luminos, definit de un unghi maxim (în radiani). O stea este considerată vizibilă dacă unghiul dintre direcția în care este îndreptată lanterna și direcția către stea, fie el , este mai mic decât acest unghi maxim . Adică, pentru ca o stea să fie vizibilă, avem:
Date de intrare
Pe prima linie se găsește un număr natural, , care reprezintă numărul de stele de pe cer, iar pe următoarele linii, se găsesc trei numere reale, , care reprezintă coordonatele stelelor. Pe următoarea linie se găsește un număr natural , numărul total de lanterne. Pe următoarele linii se găsesc câte patru numere reale, , unde primele trei sunt coordonatele în care este orientată lanterna, iar reprezintă unghiul maxim al lanternei în radieni.
Date de ieșire
Vasile dorește să afle câte dintre stelele de pe cer a reușit să vadă în această seară, chiar dacă știe deja răspunsul.
Restricții și precizări
- ;
- ;
- ;
- ;
- și are maxim 10 zecimale.
- Fiecare coordonată va avea exact două zecimale.
Exemplul 1
stdin
5
1.00 1.00 0.00
2.00 2.00 0.00
0.00 1.00 1.00
1.00 0.00 1.00
2.00 0.00 0.00
2
1.00 1.00 0.00 0.8
0.00 1.00 1.00 0.6
stdout
4
Explicație
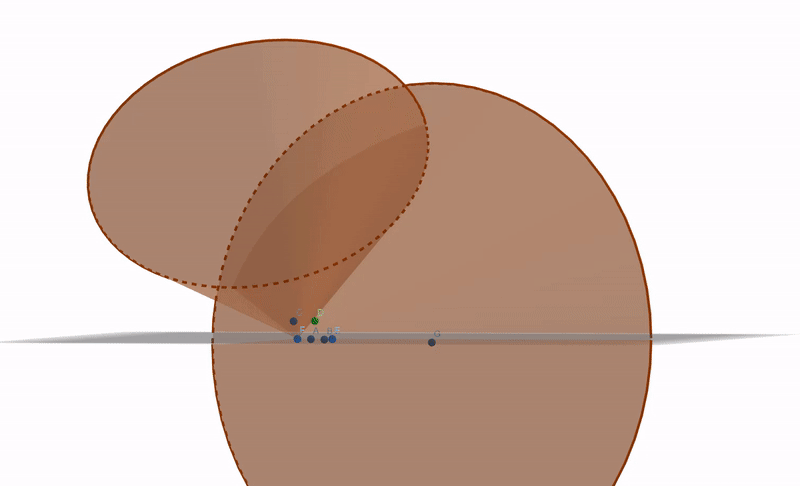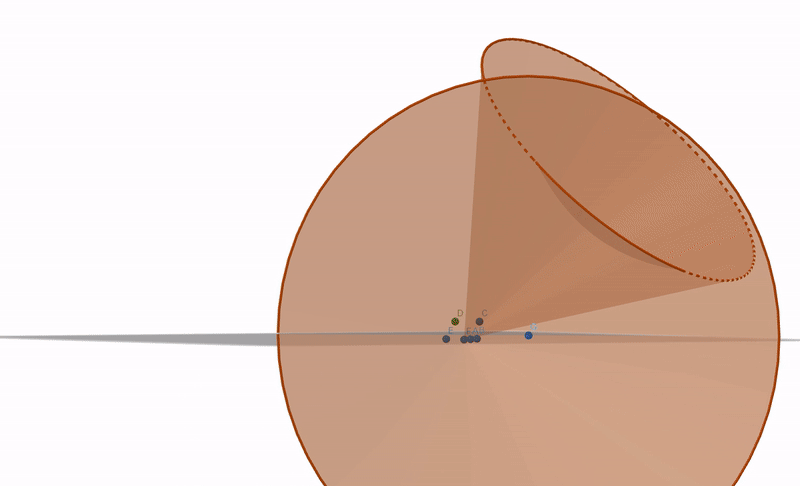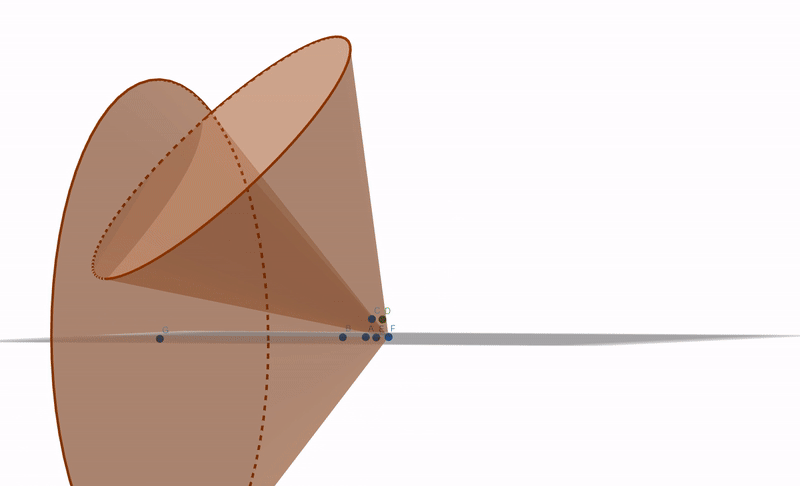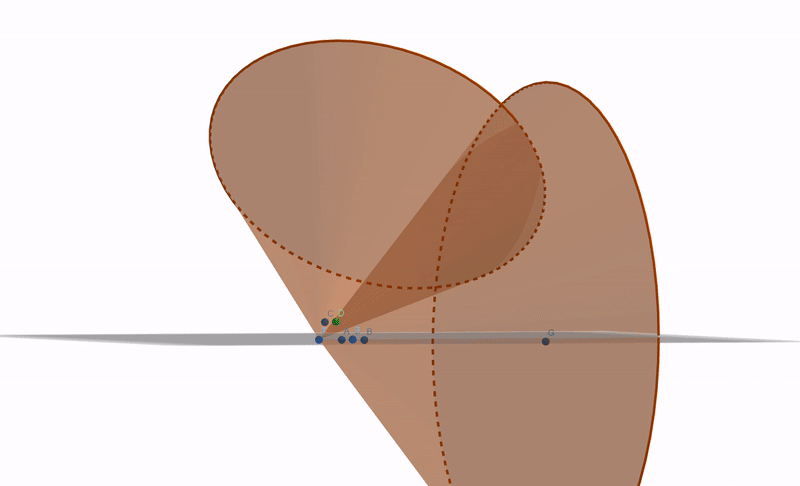
A se vedea gif-ul de sus.
Prima lanternă vede stelele A,B și E. A doua lanternă vede steaua C.