Problem 3255: Sushi Cat

Cerință

Pentru a o salva pe soția sa, Maki, Sushi Cat a ajuns într-un ~~spațiu abstract vectorial non-eucli...~~ arbore. Acesta are $N$ noduri numerotate de la $1$ la $N$ , este înrădăcinat în nodul $1$ , iar fiecare muchie are o greutate asociată. Sushi Cat "cade" de la rădăcină spre frunze. Atunci când acesta ajunge la un nod ce are mai mult de un fiu, poate cădea în oricare cu probabilitate proporțională cu valoarea muchiei către acesta. Spre exemplu, dacă un nod are doi fii și muchia spre primul fiu are cost $1$ , iar spre celălalt fiu $3$ , atunci are probabilitate $\frac{1}{1+3}$ să continue spre primul fiu, și $\frac{3}{1+3}$ spre celălalt.

Într-un final, Sushi Cat ajunge într-una din frunze. Dar nu se oprește acolo! Arborele se înrădăcinează în frunza în care tocmai a ajuns, iar jocul se repetă de încă $K$ ori. La final, el este prea amețit să știe unde s-a oprit. Așa că vă cere vouă să aflați pentru fiecare frunză a arborelui (inclusiv rădăcina, dacă are un singur vecin), probabilitatea ca el să se fi oprit acolo la finalul aventurii.

Date de intrare

Pe prima linie se găsesc numerele întregi $N$ și $K$ . Următoarele $N - 1$ linii conțin triplete de forma $(u, v, w)$ , reprezentând faptul că există o muchie bidirecțională de la nodul $u$ la nodul $v$ de greutate $w$ .

Date de ieșire

Pentru fiecare frunză a arborelui în ordine crescătoare (inclusiv rădăcina, dacă are un singur vecin), se cere probabilitatea ca Sushi Cat să se fi oprit în frunza respectivă. Dacă probabilitatea cerută este un număr real de forma $\frac{p}{q}$ , atunci se cere să se afișeze $p \cdot q^{-1} \mod 10^9 + 7$ , unde prin $q^{-1}$ am notat inversul modular al lui $q$ modulo $10^9 + 7$ .

Restricții și precizări

$2 \leq N \leq 100$ ;
$0 \leq K \leq 10^{18}$ ;
$1 \leq w \leq 10$ ;
Pentru teste în valoare de $22$ de puncte, $K=0$ ;
Pentru alte teste în valoare de $6$ de puncte, $K=1$ ;
Pentru alte teste în valoare de $12$ de puncte, arborele este un lanț;
Pentru alte teste în valoare de $29$ de puncte, $K \leq 3 \cdot 10^4$ ;
Pentru alte teste în valoare de $31$ de puncte, nu există restricții suplimentare.

Exemplul 1

stdin

stdout

0 
333333336 
666666672

Explicație

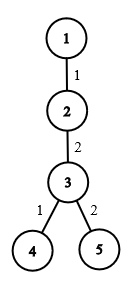
Acesta este arborele reprezentativ pentru exemplu. Sushi Cat va cădea din nodul $1$ și va ajunge cu probabilitate $1$ până în nodul $3$ . De acolo, are probabilitate $\frac{1}{3}$ să continue spre $4$ și $\frac{2}{3}$ să continue spre $5$ . Astfel, rezultatul este următorul:

Pentru frunza $1$ , probabilitate $0$ ;
Pentru frunza $4$ , probabilitate $\frac{1}{3}$ , deci vom afișa $1 \cdot 3^{-1} \mod 10^9 + 7 = 333333336$
Pentru frunza $5$ , probabilitate $\frac{2}{3}$ , deci vom afișa $2 \cdot 3^{-1} \mod 10^9 + 7 = 666666672$

Exemplul 2