The 2D map of the world has the shape of a matrix with lines and columns. On this map, the countries are labelled with numbers . The countries have the shape of a square with the side or a rectangle made of two adjacent squares with the side . There can be only one superpower, a country which is made of adjacent squares of side . Two countries can be considered neighbours if they have at least a common side.
In the scheme on the right, we have a sized map, which contains countries (the country is a superpower). Our purpose is to paint the countries on the map, so that each country should have a different colour from all its neighbours. A possible colouring is presented in the scheme on the right.
Task
Paint the countries on the map in maximum four colours, codified with , , , , so that two neighbouring countries should have different colours.
Input data
The first line contains the values of and separated by a space, representing the number of lines and the number of columns of the map. Each of the following lines contains natural numbers different from zero separated by one or more spaces, and together, they form the map of the world, with countries counted .
Output data
A matrix with lines and columns will be displayed, containing a possible painting of the map, as it is defined above. The numbers on a line will be separated from each other by a space.
Constraints and clarifications
- Any correct solution is accepted.
- A valid painting can contain or fewer colours.
- The test cases are not the same as the ones used in the contest, so the scores might be slightly different from these obtained in the real contest.
| # | Points | Constraints |
|---|---|---|
| 0 | 0 | Examples. |
| 1 | 25 | and no superpower exists. |
| 2 | 15 | and there exists a superpower. |
| 3 | 30 | and no superpower exists. |
| 4 | 30 | and there exists a superpower. |
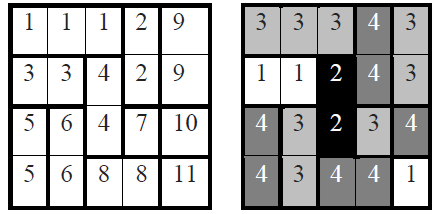
Example 1
stdin
4 5
1 1 1 2 9
3 3 4 2 9
5 6 4 7 10
5 6 8 8 11
stdout
3 3 3 4 3
1 1 2 4 3
4 3 2 3 4
4 3 4 4 1
Explanation
The countries and are painted using colour .
The country is painted using colour .
The countries , , and are painted using colour .
The countries , , and are painted using colour .
Example 2
stdin
3 3
1 2 3
5 4 9
6 8 7
stdout
1 2 1
2 1 2
1 2 1
Explanation
All the countries are squares with the side . In this case, all the countries can be painted using only two colours.