KST

A KST is a search tree which has $K$ values in every node and $K+1$ children. For example, for $K=1$ a KST becomes a binary search tree. The values inside each node are sorted in ascending order. We will write $v_i$ for the value on the position $i$ of a node. The tree has the following property: for every node, its first child will contain smaller values than $v_1$, the second child will contain values in the interval $(v_1, v_2)$, the third child will contain values in the interval $(v_2, v_3)$, $\dots$, the penultimate child will contain values in the interval $(v_{K-1}, v_K)$, and the last child will contain larger values than $v_K$.

A node cannot have children if it does not contain $K$ values. The leaves can contain even fewer than $K$ values.

Task

Given $N$ – the number of elements and $K$, the task is to find out how many such trees exist. The elements will be $1,2,3,\dots,N$. For example, the following two trees are valid for $N = 13$ and $K = 3$.

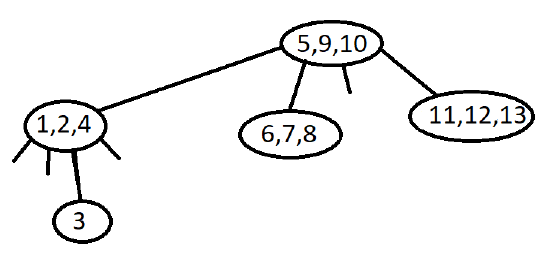
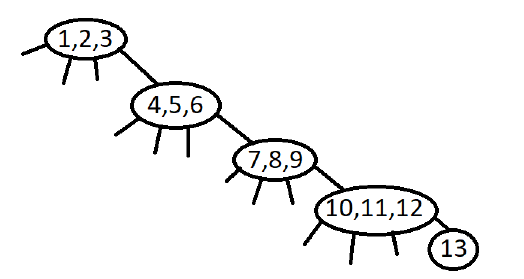
Input data

The first line contains the numbers $N$ and $K$.

Output data

The first line will display how many such trees exist, modulo $666 \ 013$.

Constraints and clarifications

• $1 \leq N, K \leq 1 \ 000$
• For $10\%$ of the testcases, $N \leq 10$ and $K \leq 4$.
• For another $15\%$ of the testcases, $N \leq 25$ and $K \leq 4$.
• For another $25\%$ of the testcases, $N \leq 1 \ 000$ and $K = 1$.

Example 1

stdin

5 1

stdout

42

Example 2

stdin

5 2

stdout

16

Example 3

stdin

666 13

stdout

581769

Example 4

stdin

987 123

stdout

529937