Time limit: 0.03s
Memory limit: 4MB
Input: arbore.in
Output: arbore.out
Se dă un arbore format din noduri numerotate de la la . Rădăcina este nodul numerotat cu și fiecare nod are asociat un număr natural nenul.
Cerință
Să se selecteze din arborele iniţial un subgraf conex pentru care suma valorilor asociate nodurilor este egală cu un număr natural dat. Un subgraf este graful din care se elimină noduri împreună cu muchiile aferente.
Date de intrare
Fişierul de intrare arbore.in, are următoarea structură:
- pe prima linie sunt scrise numerele şi ;
- pe cea de-a doua linie este scrisă valoarea asociată nodului (rădăcina arborelui);
- pe cea de-a treia linie sunt scrise două numere, primul reprezentând nodul părinte al nodului , iar al doilea reprezentând valoarea asociată nodului ;
- pe cea de-a patra linie sunt scrise două numere, primul reprezentând nodul părinte al nodului , iar al doilea reprezentând valoarea asociată nodului ;
- ...
- pe linia sunt scrise două numere, primul reprezentând nodul părinte al nodului , iar al doilea reprezentând valoarea asociată nodului .
Date de ieşire
Ieşirea se va face în fişierul arbore.out:
- dacă nu există soluţie se va afişa doar numărul pe prima linie;
- dacă există soluţie se vor afişa nodurile ce formează un subgraf conex care respectă cerinţa problemei (câte un singur nod pe fiecare linie).
Restricţii și precizări
- Valoarea asociată unui nod este un număr din intervalul .
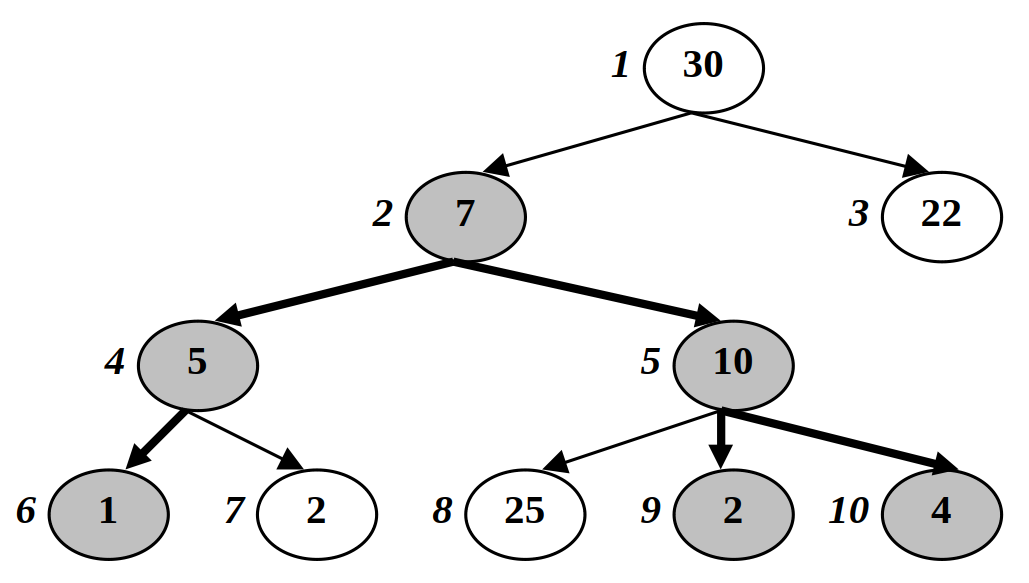
Exemplu
arbore.in
10 29
30
1 7
1 22
2 5
2 10
4 1
4 2
5 25
5 2
5 4
arbore.out
2
4
5
6
9
10
Explicație