Tocmai ați fost angajat la compania aeriană „Brătianu Airlines”. Știți că există orașe indexate de la la între care compania organizează trasee de zbor. Se dă fiecare traseu de zbor prin numărul orașului din care decolează, orașul în care aterizează, durata și prețul zborului.
Din cauza unei supraîncărcări a rețelei, cauzată de aglomerația din aeroport, trebuie să găsiți manual o metodă de a găsi zboruri pentru pasageri.
Cerință
Pentru două orașe date, și , trebuie să aflați:
- Un drum de la orașul la orașul care să aibă durată minimă, dacă există.
- Dintre toate drumurile de durată minimă de la orașul la orașul , care este prețul minim al unui astfel de drum, dacă există.
Numim drum de la un oraș la un oraș un șir , , ..., , unde și , iar pentru orice , cu , există un zbor de la la .
Definim durata unui drum , , ..., ca fiind suma duratelor zborurilor de la la , cu .
Definim prețul unui drum , , ..., ca fiind suma prețurilor zborurilor de la la , cu .
Date de intrare
Pe prima linie a fișierului de intrare zboruri.in se află cinci numere naturale nenule, în această ordine: , , , , respectiv , unde reprezintă numărul cerinței care se va rezolva, iar restul au semnificațiile din enunț.
Pe următoarele linii se află descrierile celor zboruri, câte un zbor pe linie. Al -lea zbor, cu , este dat prin patru numere naturale nenule, în această ordine:
- - orașul de decolare;
- - orașul de aterizare;
- - durata zborului;
- - prețul zborului.
Date de ieșire
Fișierul de ieșire zboruri.out va conține pe prima linie:
- Pentru , șirul , , ..., , ce reprezintă un drum de durată minimă de la orașul la orașul , dacă există. Dacă nu există niciun astfel de drum se va afișa numărul .
- Pentru , un singur număr natural , ce reprezintă prețul minim dintre prețurile tuturor drumurilor de durată minimă de la la , dacă există. Dacă nu există niciun astfel de drum se va afișa numărul .
Restricții și precizări
- , cu
- , cu
- Pentru prima cerință, dacă există mai multe drumuri de durată minimă, se va puncta oricare dintre acestea.
- Se acordă 10 puncte din oficiu.
| # | Punctaj | Restricții |
|---|---|---|
| 1 | 30 | |
| 2 | 20 | ; Există un singur drum de durată minimă |
| 3 | 40 | Fără restricții suplimentare |
Exemplul 1
zboruri.in
1 6 8 1 4
1 2 3 3
1 6 1 1
2 3 5 1
2 5 2 2
3 4 3 1
5 4 4 2
6 2 2 1
6 5 4 3
zboruri.out
1 2 5 4
Exemplul 2
zboruri.in
2 6 8 1 4
1 2 3 3
1 6 1 1
2 3 5 1
2 5 2 2
3 4 3 1
5 4 4 2
6 2 2 1
6 5 4 3
zboruri.out
6
Explicație
Zborurile din ambele exemple se pot reprezenta grafic ca în imaginea următoare:
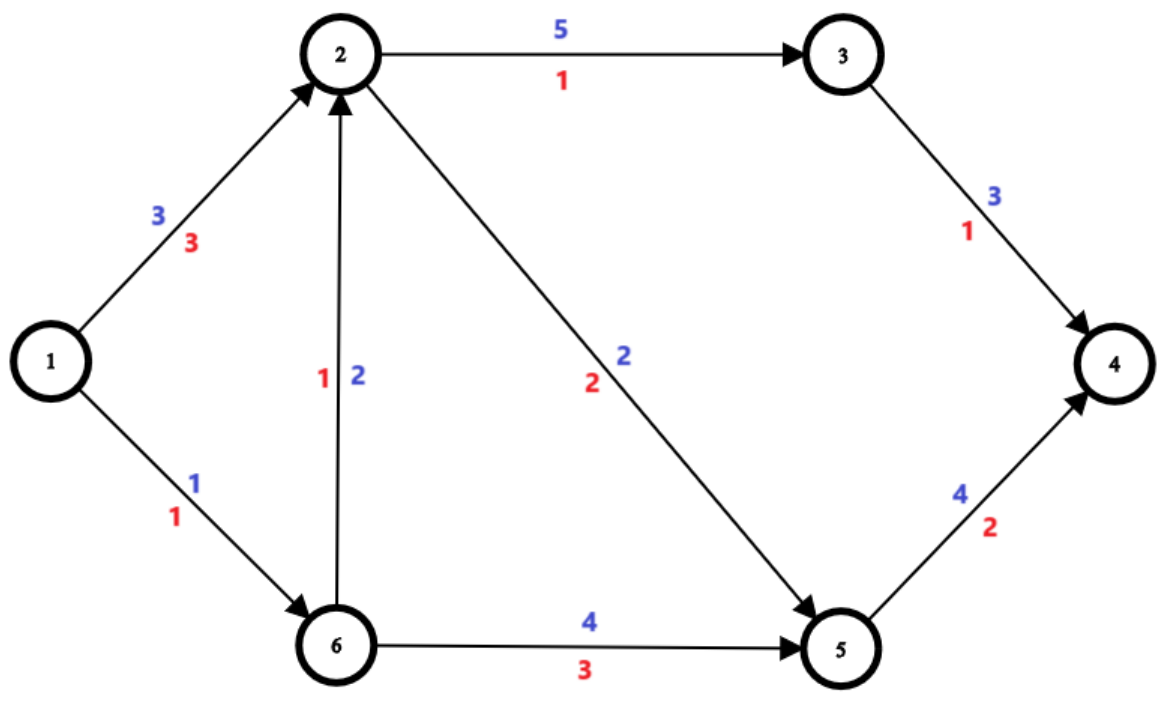
Cercurile reprezintă orașele, cu indicele lor înăuntru, și săgețile reprezintă zborurile, unde este notată cu albastru durata zborului și cu roșu prețul zborului.
Pentru primul exemplu, durata minimă a unui zbor este , iar toate zborurile cu această durată sunt:
- , , , ;
- , , , , ;
- , , , .
Oricare dintre acestea este considerat corect.
Pentru al doilea exemplu, drumurile de durată minimă de mai sus au prețurile:
- ;
- ;
- .
Astfel prețul minim al unui drum de durată minimă este .