În timp ce Victor se plimba prin pădure, i-a fost atrasă atenția de un copil ce se juca pe trotuar.
El sărea de pe primul pătrat, care avea un număr scris cu creta în interior, pe un alt pătrat, cu alt număr scris, și tot așa până la al -lea pătrat, aflat la finalul desenului. Pentru a face jocul mai interesant, bunicul lui i-a dat următoarea provocare:
Acesta a observat fiecare număr aflat pe al -lea pătrat, cu , și i-a spus că, pornind de pe primul pătrat, la fiecare săritură, îi va da atâtea bomboane cât diferența dintre numărul de pe pătratul pe care a ajuns și numărul de pe pătratul de pe care a sărit, totul la pătrat. Mai formal:
,
cu semnificațiile:
- = Numărul de bomboane pe care i le va da bunicul la o săritură
- = Numărul aflat pe pătratul pe care a ajuns
- = Numărul aflat pe pătratul de pe care a sărit
Băiatul poate sări doar în față și se poate opri din sărit oricând este mulțumit cu numărul de bomboane obținute.
Cerință
Știind numărul de pătrate, , numerele de pe fiecare pătrat, , , ..., , și că nepotul poate, în orice moment, să sară câte maximum pătrate, calculați numărul maxim de bomboane pe care le poate obține.
Date de intrare
Pe prima linie a fișierului de intrare sarituri.in se află două numere naturale nenule, și , cu semnificația din enunț.
Pe a doua linie se află numere naturale, , , ..., , cu semnificația din enunț.
Date de ieșire
Pe prima linie a fișierului de ieșire sarituri.out se va afișa un singur număr natural, care reprezintă răspunsul la cerința dată.
Restricții și precizări
- , cu
- Se acordă 10 puncte din oficiu.
Exemplul 1
sarituri.in
4 1
3 6 1 2
sarituri.out
35
Explicație
Copilul poate sări câte maximum un singur pătrat, deci șirul de sărituri este:
:
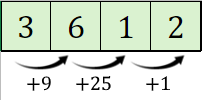
Este evident că suma maximă este , relație egală cu:
.
Exemplul 2
sarituri.in
5 2
2 3 8 7 2
sarituri.out
72
Explicație
Copilul poate sări câte maximum două pătrate, deci săriturile pot fi:
Se observă că șirul ce obține suma maximă este:
.
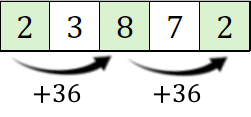
Astfel, se obține suma maximă: , relație egală cu: