You are given a tournament graph (a complete directed graph) of vertices, numbered from to . Initially, all edges are directed towards the vertex with the higher number.
A triangle is a triplet of vertices , such that there are edges , , in the graph,
with and , , .

You need to process updates, where in each update we flip an edge. The updates are permanent, and you are required to count the number of triangles in the graph following each update.
Input data
The first line of the input contains and , representing the number of vertices in the graph and the number of updates.
The next lines contain the updates in the form , meaning that the edge between and is to be flipped. It is guaranteed that the edge between and in the graph is directed towards right before the update.
Output data
The output must contain lines, the number of triangles after each update.
Constraints and clarifications
- .
- .
- and for each .
| # | Points | Constraints |
|---|---|---|
| 1 | 0 | Examples |
| 2 | 14 | |
| 3 | 16 | |
| 4 | 23 | |
| 5 | 47 | No additional constraints |
Example
stdin
4 4
2 4
1 2
4 2
2 3
stdout
1
2
0
1
Explanation
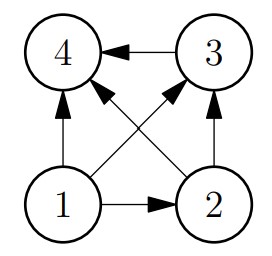
In the sample case, the initial graph (without updates) is diplayed in the figure below.
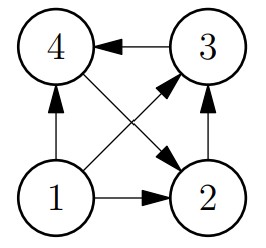
The first update flips edge . The resulting graph contains only one triangle (see below).
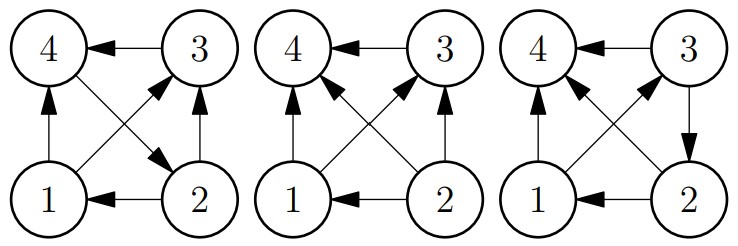
The graphs obtained after each remaining update are displayed in the following figure (from left to right).