fft2d

Un graf FFT de ordin $F$ este un graf orientat cu $F$ niveluri, numerotate de la $0$ la $F - 1$. Fiecare nivel este compus din $2^{F - 1}$ noduri, numerotate cu numere de la $0$ la $2^{F - 1} - 1$. Vom folosi notația $(h, x)$ pentru a ne referi la nodul cu indicele $x$ de pe nivelul $h$.

Muchiile grafului FFT sunt următoarele:

1. Toate muchiile orientate de la $(h, x)$ la $(h + 1, x)$;
2. Toate muchiile orientate de la $(h, x)$ la $(h + 1, x \oplus 2^{F - h - 2})$.

Inițial toate nodurile grafului au fost colorate de Stiuboss cu alb. De supărare, Nustiuboss a selectat $T$ noduri pe care le-a colorat cu negru. (Vedeți figura)

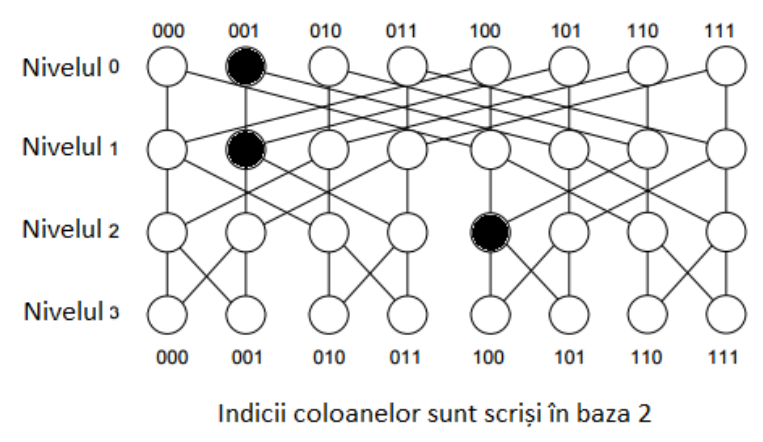
Intrigat de modificările făcute, Nusdeaici s-a decis să calculeze numărul de perechi $(a, b)$ cu proprietatea că există măcar un drum orientat de la nodul $(0, a)$ la nodul $(F - 1, b)$ care nu trece prin niciun nod negru.

Date de intrare

Fișierul de intrare fft2d.in va conține pe prima linie două numere naturale $F$ și $T$. Următoarele $T$ linii vor conține câte o pereche $(h, x)$, reprezentând faptul că nodul de pe nivelul $h$ cu indicele $x$ este colorat cu negru.

Date de ieșire

Fișierul de ieșire fft2d.out va conține un singur număr natural reprezentând numărul de perechi $(a, b)$ cu proprietatea că există măcar un drum orientat de la nodul $(0, a)$ la nodul $(F - 1, b)$ care nu trece prin niciun nod negru.

Restricții

• $1 ≤ F ≤ 30$
• $1 ≤ T ≤ 100 \ 000$
• $A \oplus B$ reprezintă operația de sau exclusiv pe biți (xor).
• ATENȚIE! Muchiile sunt orientate (deși în figură nu sunt reprezentate astfel).
• “Apam, cum să numim personajul principal?” Răspuns: “Nustiuboss”.
• Pentru teste în valoare de $10$ puncte, $F ≤ 10$
• Pentru alte teste în valoare de $10$ puncte, $F ≤ 16$
• Pentru alte teste în valoare de $30$ puncte, $T ≤ 2 \ 000$

Exemplul 1

fft2d.in

3 3
0 2
1 1
2 3

fft2d.out

5

Explicație

Există $5$ perechi $(a, b)$ cu proprietatea din enunț. Mai exact, acestea sunt: $(0, 0)$, $(0, 1)$, $(0, 2)$, $(1, 2)$, $(3, 2)$.

Exemplul 2

fft2d.in

4 3
0 1
1 1
2 4

fft2d.out

44 

Explicație

Există $44$ de perechi $(a, b)$ cu proprietatea din enunț. Figura de mai sus corespunde acestui exemplu.

Exemplul 3

fft2d.in

15 10
3 12914
8 10479
12 1039
8 13597
11 2633
12 10668
12 6769
11 4443
7 15697
12 13418

fft2d.out

268271648

Explicație

Va trebui să ne credeți pe cuvânt.