Task
The final round of IIOT is approaching and after solving so many tree problems during the previous edition of the contest, you start to wonder what the next tree problem is going to be. Your instincts were spot-on, finally here is a tree problem for you to solve!

You are given a tree graph with nodes, rooted at vertex .
We define the -th ancestor of a vertex as the node we reach if we move steps up the tree, in the direction of the root.
If we reach the root before doing steps, then we say that the -th ancestor does not exist.
For a fixed integer , your task is to find the -th ancestor of each node in the tree, or report that it doesn't exist.
Input data
The input file consists of:
- a line containing integers , .
- lines, the -th of which consisting of integers , , representing an edge between nodes and .
Output data
The output file must contain a single line consisting of the integers, representing the -th ancestors of each node, or if it does not exist.
Constraints and clarifications
- .
- and for each .
| # | Score | Constraints |
|---|---|---|
| 1 | 0 | Examples. |
| 2 | 25 | . |
| 3 | 16 | . |
| 4 | 59 | No additional limitations. |
Example
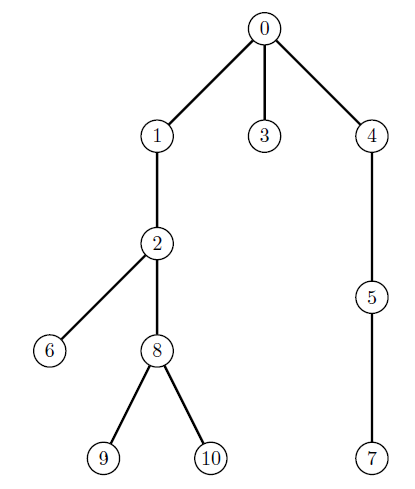
stdin
11 2
0 3
1 2
0 4
0 1
2 6
4 5
5 7
2 8
8 9
8 10
stdout
-1 -1 0 -1 -1 0 1 4 1 2 2
Explanation
The tree in the sample test case is displayed in the following figure.