Planning Excursions

Task

Adrian is starting a new business as a travel counsellor, helping tourists to plan their trip along the Amazon River!

Along the river, there are $N$ boat excursions available, the $i$-th of which starting at $L_i$ meters from the river source and ending at $R_i$ meters from the river source.
All excursions follow the water flow, in order to keep the engines turned off and ensure a full immersion in the natural environment.

Tourists are often puzzled by the huge number of available options. So, they call Adrian for suggestions! There are $Q$ requests from tourists. The $i$-th request comes from
a tourist standing at $X_{i}$ meters from the river source. That tourist wants to plan a series of trips that brings him to the farthest possible distance $Y_i$ from the river source,
using a tourist pass that allows to do at most $V_{i}$ excursions. Furthermore, the tourist wants to do at least $U_i$ excursions,
and does not want to repeat an excursion.
The chosen excursions must be perfectly consecutive: each of them must start where the previous one has ended, with the first one starting at $X_i$ and the last one ending in $Y_i$.
In case it is impossible to plan a series of at least $U_i$ excursions, we conventionally set $Y_i$ to $-1$. Help Adrian answer the tourists' requests!

Input data

The input file consists of:

• a line containing integer $N$.
• $N$ lines, the $i$-th of which consisting of 64-bit integers $L_{i}$, $R_{i}$.
• a line containing integer $Q$.
• $Q$ lines, the $i$-th of which consisting of 64-bit integer $X_{i}$ and integers $U_{i}$, $V_{i}$.

Output data

The output file must contain a single line consisting of the $Q$ integers $Y_{0}, \, \ldots, \, Y_{Q-1}$.

Constraints and clarifications

• $1 \le N \le 1 \ 000$.
• $1 \le Q \le 100 \ 000$.
• $0 \le L_i \le R_i \le 10^{18}$.
• $0 \le X_i \le 10^{18}$.
• $0 \le U_i \le V_i \le N$.

Example 1

stdin

5
0 2
0 4
2 5
4 10
5 6
3
0 0 3
0 3 3
2 1 5

stdout

10 6 6

Explanation

In the first sample case, the available excursions are as follows:

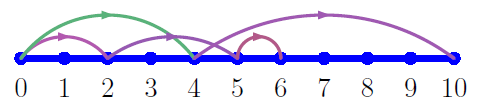
The first tourist stands at $X_0 = 0$, and wants to perform a number of excursions from $0$ to $3$. The farthest he can reach is through the two excursions $0 \rightarrow 4 \rightarrow 10$, thus $Y_0 = 10$.
The second tourist also stands at $0$, but wants to perform exactly $3$ excursions: his only option is the trip $0 \rightarrow 2 \rightarrow 5 \rightarrow 6$.
The last tourist stands at $2$, and wants to perform a number of excursions between $1$ and $5$. His best option is the trip $2 \rightarrow 5 \rightarrow 6$.

Example 2

stdin

5
4 4
2 4
4 4
4 7
2 4
4
2 4 4
2 5 5
1 0 2
1 1 5

stdout

7 -1 1 -1

Explanation

In the second sample case, the available excursions are as follows:

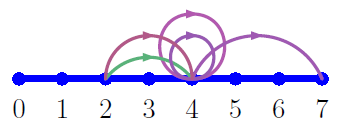
The first tourist stands at $2$, and wants to perform exactly $4$ excursions: his only option is the trip $2 \rightarrow 4 \rightarrow 4 \rightarrow 4 \rightarrow 7$.
The second tourist also stands at $2$, but wants to perform exactly $5$ excursions: this is not possible, so the answer is $Y_1 = -1$.
The third tourist stands at $1$, and wants to perform a number of excursions from $0$ to $2$. His only possibility is to perform $0$ excursions, staying at $Y_2 = 1$, since there are no excursions starting from $1$.
The last tourist also stands at $1$, but wants to perform at least one excursion, which is not possible, so the answer is $Y_3 = -1$.