Mugurel a decis să devină în sfârșit cel mai mare antreprenor din „Imperiul Rațelor de Cauciuc”. Astfel, el și-a deschis o afacere cu fructele sale preferate: portocale și banane.
Acesta primește planul recoltelor de fructe: timp de zile, în fiecare zi Mugurel primește grămezi de portocale și grămezi de banane, reprezentate prin numărul lor de kilograme. Mugurel trebuie să împacheteze toate aceste fructe, însă producătorul său de cutii îi oferă două variante, din care poate alege doar una: fabricarea a cutii pentru portocale și cutii pentru banane (împachetare separată), sau fabricarea a cutii mixte (împachetarea portocalelor și a bananelor împreună). Există însă niște reguli privind împachetarea:
- O cutie poate conține doar grămezi de fructe consecutive (o grămadă trebuie pusă în cutie înainte ca o altă grămadă de același tip să vină).
- O grămadă de fructe nu poate fi separată în mai multe grămezi.
- Orice cutie deschisă trebuie închisă la finalul unei zile (pe scurt, o cutie nu poate conține fructe din zile diferite).
- Cutiile mixte trebuie să conțină același număr de grămezi de portocale și banane (nu neapărat același număr de kilograme).
Însă, totul are un preț. Fie , , capacitățile cutiilor de portocale, banane respectiv mixte. Atunci, Mugurel va plăti sau , în funcție de varianta de împachetare aleasă. Mugurel va alege metoda de împachetare astfel încât suma de bani cheltuită să fie cât mai mică.
După ce plătește și primește cutiile, începe împachetarea. De fiecare dată când închide o cutie, o pune la finalul șirului de cutii deja închise (Mugurel se ocupă mai întâi de grămada de portocale, apoi de cea de banane). La finalul împachetării fructelor, el trebuie să împartă șirul de cutii în două șiruri consecutive, pe care le vom numi loturi.
Cerință
Loturile vor fi trimise către cele două cetăți ale Imperiului, însă Mugurel nu vrea să pornească un război între cele două cetăți, așadar vrea să le împartă cu grijă. Numim discrepanță a unui lot diferența dintre cutia cu număr maxim de kilograme și cea cu număr minim. Împărțirea trebuie făcută astfel încât suma discrepanțelor celor două loturi să fie minimă, pentru împachetare.
Cu atâtea responsabilități pe cap, Mugurel vă roagă să-l ajutați cu afacerea.
Date de intrare
Prima linie conține două numere întregi, și , reprezentând numărul de zile și numărul de grămezi zilnice.
A doua linie conține numerele întregi , , , , reprezentând numărul de cutii care se fabrică de un anumit tip, precum și prețurile celor trei tipuri de cutii.
Următoarele linii conțin câte numere întregi, reprezentând kilogramele grămezilor de portocale, în ordinea în care acestea vin.
Următoarele linii conțin câte numere întregi, reprezentând kilogramele grămezilor de banane, în ordinea în care acestea vin.
Date de ieșire
Prima linie va conține un singur număr, , reprezentând suma de maci pe care Mugurel trebuie să o cheltuie pentru toate cutiile.
A doua linie va conține un singur număr, , reprezentând numărul total de cutii închise cu fructe.
Următoarele linii vor conține datele cutiilor în ordinea în care au fost închise, pe fiecare linie aflându-se câte două valori: numărul de kilograme din cutia respectivă, precum și tipul cutiei, reprezentat de un singur caracter (P pentru portocale, B pentru banane, M pentru mixt).
Ultima linie va conține un singur număr, , reprezentând suma minimă a discrepanțelor celor două loturi care se poate obține în urma unei împărțiri a șirului de cutii format din împachetarea aleasă.
Restricții și precizări
- Fiecare grămadă de fructe conține cel mult kilograme.
- Cutiile de tipuri diferite pot avea o capacitate diferită, însă toate cutiile folosite cu același scop (portocale, banane, mixte) au aceeași capacitate.
- Nu este necesar ca toate cutiile să fie folosite (însă suma cheltuită rămâne aceeași), deci pentru împachetare mixtă și pentru împachetare separată.
- Fiecare lot trebuie să conțină cel puțin o cutie, însă cutia minimă poate să coincidă cu cutia maximă. Se garantează că șirul de cutii rezultat în urma împachetării este format din cel puțin două cutii.
- Dacă există mai multe soluții corecte, se poate afișa oricare dintre acestea.
- Macul este moneda oficială din Imperiul Rațelor de Cauciuc.
- Pentru teste în valoare de puncte, .
- Pentru alte teste în valoare de puncte, .
- Pentru alte teste în valoare de puncte, toate grămezile au același număr de kilograme.
- Pentru alte teste în valoare de puncte, , iar suma grămezilor din fiecare zi este kilograme.
- Pentru alte teste în valoare de de puncte, .
- Pentru alte teste în valoare de de puncte, nu există restricții suplimentare.
Exemplul 1
mugurel.in
2 4
4 2 3 7
2 9 9 1
10 9 8 9
2 3 5 3
20 19 13 4
mugurel.out
98
8
11 P
10 P
13 B
20 B
19 P
19 B
17 P
17 B
6
Explicație
În primul exemplu, cel mai ieftin va fi să împachetăm fructele în cutii separate. Una dintre împachetările posibile în care vom cheltui o sumă minimă de maci ar fi (cu portocaliu marcăm portocalele, iar cu galben bananele):

În urma acestei împachetări, obținem următorul șir de cutii:
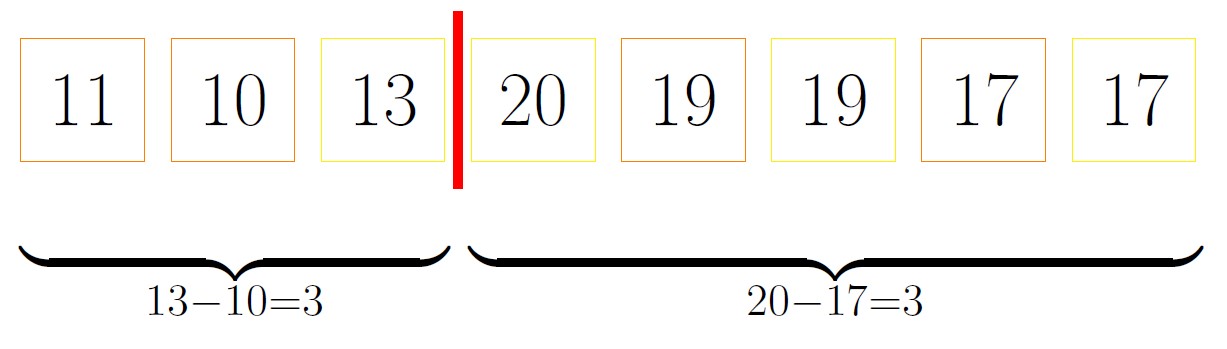
Astfel, capacitatea cutiilor de portocale va fi de , iar capacitatea celor pentru banane va fi de . Prețurile cutiilor sunt de pentru portocale și pentru banane, cheltuind astfel: .
Împărțirea optimă în cele două loturi este dată de linia roșie, obținând suma minimă a discrepanțelor: .
Exemplul 2
mugurel.in
3 3
5 14 18 7
2 2 2
3 3 3
4 5 7
1 1 4
3 3 3
6 1 8
mugurel.out
112
5
12 M
6 M
12 M
16 M
15 M
7
Explicație
În al doilea exemplu, pentru a cheltui cât mai puțini bani, fructele trebuie împachetate împreună. O împachetare posibilă ar fi:
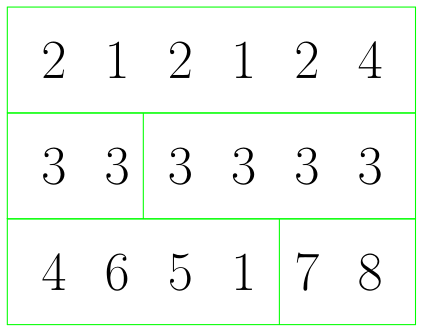
Se observă că numărul de grămezi de portocale este egal cu numărul de grămezi de banane pentru fiecare cutie. Obținem astfel următorul șir de cutii:
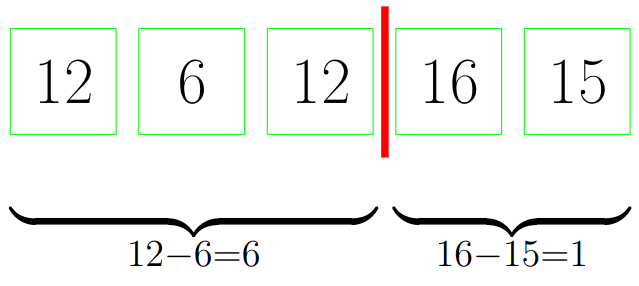
Astfel, capacitatea cutiilor mixte va fi de . Prețul cutiei este de , cheltuind astfel: .
Împărțirea optimă în cele două loturi este dată de linia roșie, obținând suma minimă a discrepanțelor: .