Azusa, the witch of the highlands, wants to do a fun activity with her friend Laika: gardening. They want to make a rectangular garden meters tall by meters wide. The garden is divided into meter by meter squares. The question is: what flowers should they plant?
Laika has found different types of flowers. Azusa and Laika will plant one type of flower in each meter by meter square. Furthermore, for aesthetic reasons, the garden must satisfy the following constraints:
- Each flower type must appear at least once in the garden.
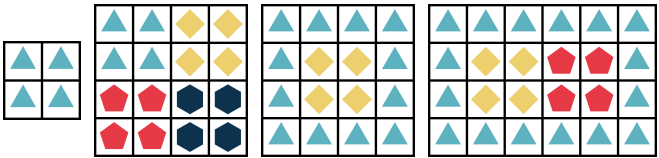
- For any two squares where the same flower type is planted, a path between them where all the intermediate squares have the same type of flower must exist. For example, the following gardens are not allowed:
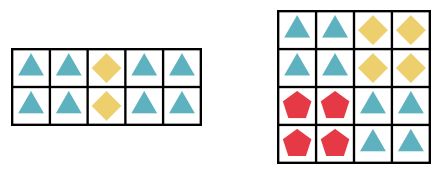
- Any square must have exactly two adjacent squares planted with the same type of flower. For example, the following gardens are not allowed:

Note that, in the previous constraints, two squares are “adjacent” if and only if they share a common edge (not merely a corner); and a path is a sequence of adjacent squares.
You are given different values for and . Help Azusa and Laika create gardens that satisfy the conditions for each test case — or, tell them that it is impossible to do this.
Input data
The first line of the input contains the integer . Afterwards, lines follow, each describing a test case. Each test case consists of three integers and .
Output data
Output the answers for each test case in order. For a test case, if no solution exists, output NO on a single line. Otherwise, first output YES on a single line, and then output integers arranged in lines and columns describing the required garden. The lines and columns of the output correspond to the lines and columns of the garden, with each integer corresponding to a meter by meter square. The integers represent the types of flowers planted in the squares, where the types are indexed from to . If there are multiple correct solutions you may output any of them.
Restrictions
- Let equal the sum of for all the test cases in a file for which an answer exists (i.e. where the output is not
NO).
| # | Points | Restrictions |
|---|---|---|
| 1 | 5 | |
| 2 | 6 | |
| 3 | 10 | |
| 4 | 18 | |
| 5 | 39 | is chosen uniformly at random between 1 and |
| 6 | 22 | No further restrictions. |
Examples
stdin
5
2 2 2
2 2 1
4 4 4
4 4 2
4 6 3
stdout
NO
YES
1 1
1 1
YES
1 1 2 2
1 1 2 2
3 3 4 4
3 3 4 4
YES
1 1 1 1
1 2 2 1
1 2 2 1
1 1 1 1
YES
1 1 1 1 1 1
1 2 2 3 3 1
1 2 2 3 3 1
1 1 1 1 1 1
Explanations
For the first test case, we note that no by garden with types of flowers is possible. Thus we output NO. The other gardens are pictured below: