Paths

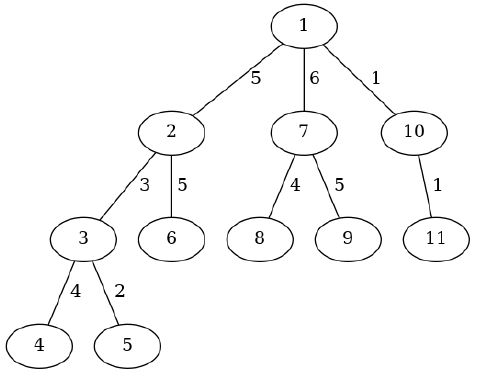
Orange the Cat found a tree (an undirected connected acyclic graph) with $N$ vertices numbered from $1$ to $N$. On each edge $i \ (1 \leq i < N)$ connecting vertices $x_i$ and $y_i$ there are $c_i$ special cat treats.

Task

Orange can choose exactly $K$ vertices, walk from the root of the tree to each of the chosen vertices along the paths from the root to the respective vertices and take all the cat treats along those paths. Of course, he can only take the treats on each edge once. Because Orange is a curious cat, he wants to know the maximum possible number of treats he could take by choosing the $K$ vertices optimally, if the root of the tree were vertex $i$, for each $i$ from $1$ to $N$.

Input

The first line of the input contains two integers $N$ and $K$, the number of vertices of the tree and the number of vertices Orange will choose, respectively. The next $N - 1$ lines contain three integers each, $x_i, y_i$ and $c_i$, describing the edges of the tree.

Output

On line $i$ for $1 \leq i \leq N$ output the maximum number of treats Orange could take if the root of the tree were vertex $i$.

Restrictions

• $1 \leq K \leq N \leq 100 \ 000$
• $0 \leq c_i \leq 1 \ 000 \ 000 \ 000$, for $1 \leq i < N$

Example

stdin

11 3
1 2 5
2 3 3
2 6 5
3 4 4
3 5 2
1 7 6
7 8 4
7 9 5
1 10 1
10 11 1

stdout

28
28
28
32
30
32
28
32
32
29
30

Explanation

If the root is vertex $1$, then Orange can choose vertices $4, 6$ and $9$. The paths from the root to the chosen vertices are $1 − 2 − 3 − 4, 1 − 2 − 6, 1 − 7 − 9$ and the number of treats along those paths is $5 + 3 + 4 + 5 + 6 + 5 = 28$. Note that the treats on edge $1 − 2$ are only counted once.