The noble Stegan, a prince of Dendromark, was left with sorrow by passing of his beloved father. After tiresome and useless struggles to find out what fate his father met by computing the area of various trapezoid figures using Simpson's rule, when all hope was lost, a spirit came to his aid. And the spirit gave him a tree to harness and take into his care. And the spirit later told him: Look! Look closer! Do you see? This tree is special as it has an even number of vertices. Should you be able to find the best manner in which to pair these vertices so that the total cost of this pairing is as small as possible, you shall find how the passing of you father came to be. But first you shall figure out what is the cost of a pairing; its secret lies in the meaning of life.
Stegan, a great mathematician that he happens to be, knows that the true meaning of life can be found in the words: "To be xor not to be" (and in the lines that followed it, but that is of no concern to us). Therefore he deduced that, for a pair of vertices, the cost of their pairing is the bitwise xor of the weights of the edges that lie on the simple path that connects the two vertices.
Unfortunately, providence has not gifted Stegan with computer science skills and so he has not a clue how to come by the solution to his problem and he has come to you to beg for help.
Formally, you are given tree with vertices, where is even. Every edge has a weight. For a pair of vertices we define the cost to pair them up to be the bitwise of the weights of the edges that lie on the simple path that connects the two vertices.
You have to find a way to split the vertices into pairs such that the total sum of their costs is as small as possible. Because it might be too hard to ask you to find the actual minimum solution, we only ask you to do your best and you will receive points accordingly.
Input
The first line of the input contains an even integer, — the number of vertices in the tree. Each of the next lines will consist of space-separated numbers meaning that there is an edge of weight that connects and . Both and are between and .
Output
On the first line, you should print the total cost of the pairs of vertices you have chosen. On the next lines, on each line you should print the indexes of nodes that should be paired together. All pairs must not have any common nodes.
Scoring
For each group:
- If there is a test case for which your program doesn't generate a valid response (Time Limit Exceeded, Runtime Error) then you will receive points for that group.
- A response is not considered valid as well if the pairs that you output are not a split of the NN nodes or do not correspond with the total cost that you output.
- If none of the above happen, then you will receive points according to the formula:
, where:
- goes through all the test cases in the test group
- is the cost that your solution computes for test case
- is the optimal answer for test case
Constraints and notes
- is even
- The bitwise (^) operator returns a number whose binary representation has a in each bit position for which the corresponding bits of either but not both operands are .
| # | Puncte | Restricții |
|---|---|---|
| 1 | 3 | |
| 2 | 6 | |
| 3 | 19 | |
| 4 | 8 | |
| 5 | 41 | |
| 6 | 23 | No further restrictions. |
Example 1
stdin
6
5 2 42
5 4 52
6 3 26
4 6 39
1 6 15
stdout
54
1 6
3 5
4 2
Explanation

Example 2
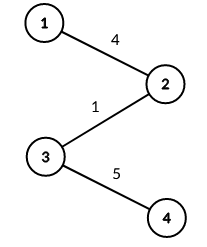
stdin
4
1 2 4
3 4 5
2 3 1
stdout
1
2 3
1 4
Explanation