Time limit: 0.2s
Memory limit: 256MB
Input:
An AA tree is a binary search tree with a special structure. Every node has a value and a level. Values obey the usual binary search tree properties:
- The value of every left child (and every node in the subtree of the left child) is less than or equal to the value of its parent.
- The value of every right child (and every node in the subtree of the right child) is greater than or equal to the value of its parent.
Levels obey the following rules:
- The level of every leaf node is .
- The level of every left child is exactly one less than that of its parent.
- The level of every right child is equal to or one less than that of its parent.
- The level of every right grandchild is strictly less than that of its grandparent.
- Every node of level greater than one has two children.
Below are five examples of AA trees, having , , , and nodes respectively. For clarity, right children on an equal level with their parent are shown in red.
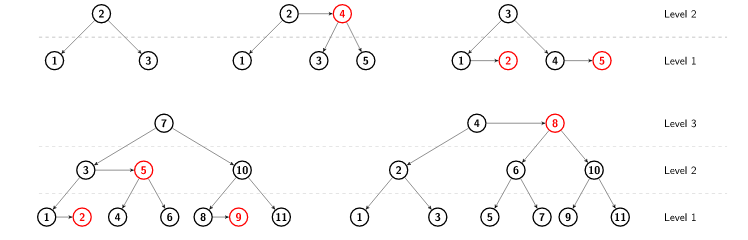
Task
Given two numbers and , how many ways are there of arranging the values , , ..., in an AA tree such that it has exactly levels?
Input data
The only line of input will contain the integers and separated by a space.
Output data
Output the number of arrangements modulo .
Constraints and clarifications
- The problem statement is slightly modified due to an error in the definition of what a binary search tree is in the original statement.
| # | Points | Constraints |
|---|---|---|
| 0 | 0 | Examples |
| 1 | 19 | |
| 2 | 34 | |
| 3 | 47 | No additional constraints |
Example 1
stdin
5 2
stdout
2
Explanation
The two possible arrangements are shown in images and above.
Example 2
stdin
442 6
stdout
896944318
Example 3
stdin
7133 9
stdout
980381648