Definim mulțimea punctelor laticiale ca fiind mulțimea perechilor de puncte din plan cu proprietatea că și sunt numere întregi.
Fie un număr natural pozitiv și cercul cu centrul în originea sistemului de axe, de rază . Notăm cu , , , , punctele laticiale care se găsesc pe cercul , în ordine inversă a acelor de ceasornic, începând cu punctul de coordonate . Să se scrie un program care determină numărul punctelor laticiale cu proprietățile:
- se găsesc în interiorul sau pe cercul ;
- nu se găsesc în interiorul sau pe laturile poligonului .
Exemplu
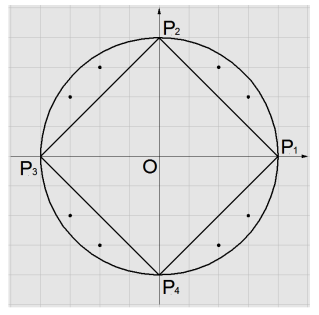
Pentru există puncte cu proprietățile cerute, conform figurii alăturate.
Date de intrare
Fişierul de intrare points.in conţine pe prima linie numărul , cu semnificaţia de mai sus.
Date de ieșire
Fişierul de ieşire points.out va conţine pe prima linie numărul , cu semnificaţia de mai sus.
Restricții și precizări
- ;
Exemplul 1
points.in
4
points.out
8
Explicație
Pe cercul se găsesc următoarele puncte laticiale , , , . Numărul punctelor laticiale situat în interiorul sau pe cercul și în exteriorul poligonului este .
Exemplul 2
points.in
764123
points.out
666556106540
Explicație
Există puncte ce verifică cerințele din enunțul problemei.