În săptămâna Altfel - ”Să știi mai multe, să fii mai bun”, elevii și se joacă un joc altfel, joc numit „margi”. Cei doi au la dispoziție o matrice pătratică binară de dimensiune .

Desfășurarea jocului este următoarea:
- jocul începe la nivelul , când se împarte matricea inițială în matrici disjuncte de dimensiunea ;
- fiecare dintre cei doi jucători alege o matrice dintre cele și adună la punctajul său numărul de valori de conținut de matricea aleasă. Dacă ambii jucători aleg aceeași matrice doar jucătorul adună la punctajul său numărul de valori de din matrice;
- pentru fiecare nivel, după împărțirea matricei inițiale, matricele rezultate vor fi numerotate asemănător figurii alăturate;
- la nivelul fiecare dintre matricele alese de jucători se împart în matrici disjuncte de dimensiunea . Fiecare dintre cei doi jucători aleg o matrice din cele noi formate.
- pentru fiecare nivel jucat fiecare jucător trebuie să aleagă o matrice;
- jocul continua cu nivelele , , etc;
- jocul se termină când dimensiunea matricelor alese este ;
Scopul jocului este obținerea sumei maxim posibile prin adunarea punctajelor celor doi jucători. Dacă există mai multe posibilități de obținere a acestei sume, fiecare jucător va alege matricele cu număr de ordine mai mic. Exemplu: pentru , vom simula un joc:
- Jucătorul
Alege matricea ce are colțul stânga-sus în (), numerotat cu . Punctaj .
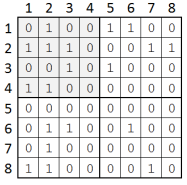
- Jucătorul
Alege matricea ce are colțul stânga-sus în (), numerotat cu . Punctaj .
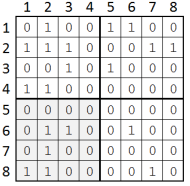
- Jucătorul
Alege matricea ce are colțul stânga-sus în (), numerotat cu . Punctaj
- Jucătorul
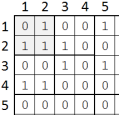
Alege matricea ce are colțul stânga-sus în (), numerotat cu . Punctaj
- Jucătorul
Alege matricea ce are colțul stânga-sus în (), numerotat cu . Punctaj .
Jucătorul a obținut , secvența alegerilor efectuate fiind: , , .
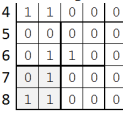
- Jucătorul
Alege matricea ce are colțul stânga-sus în (), numerotat cu . Punctaj
Jucătorul a obținut , secvența alegerilor efectuate fiind: , , .
Cerinţă
Pentru un număr natural dat și o matrice binară de dimensiunea , se cere să se determine punctajul maxim obținut de cei doi jucători. Se cere și determinarea unei strategii de alegere a matricelor la fiecare pas care să ducă la obținerea punctajului maxim.
Date de intrare
Fişierul de intrare margi.in conţine pe prima linie un număr natural . Pe linia a doua se află un număr natural . Pe următoarele linii, elementele matricei binare.
Date de ieșire
Fişierul de ieșire margi.out conţine pe prima linie suma maximă care se poate obține prin însumarea punctajelor celor doi jucători. În cazul în care în fișierul de ieșire va apărea doar această valoare. Dacă fișierul de ieșire va conține, în continuare:
Pe cea de-a doua linie se vor scrie numere ce reprezintă secvența de matrici alese de jucătorul .
Pe cea de-a treia linie se vor scrie numere ce reprezintă secvența de matrici alese de jucătorul .
Secvențele de matrici alese de cei doi trebuie să respecte următoarele două condiții:
- suma celor două punctaje obținute de cei doi jucători este maximă. Pot exista mai multe secvențe de matrici care au suma maximă.
- Fie , , , secvențele de matrici alese de , respectiv , , , , secvențele de matrici alese de , la nivelele , , , , . Dacă compunem șirul , , , , , , , , , dintre toate șirurile posibile care dau suma maximă, trebuie ales cel șirul minim lexicografic.
Restricții și precizări
- poate fi sau
- Spunem că șirul este mai mic lexicografic decât șirul , dacă există o poziție , astfel încât = , = , , = , iar < .
- Pentru teste în valoare de de puncte avem .
Exemplul 1
margi.in
1
2
0000
0100
0000
0000
margi.out
2
Explicație
Suma maximă = ( + ) + ( + ) = . Dacă am fi avut , pe liniile și ar mai fi apărut:
1 1
1 4
Exemplul 2
margi.in
2
3
01001100
11100011
00101000
11000000
00000000
01100100
01000000
11000010
margi.out
20
1 1 2
3 3 2
Explicație
Suma maximă = () + () + () = . Exemplul din figura de mai sus.