Se consideră o tablă de şah cu linii şi coloane, şi . Liniile acestei table sunt numerotate de sus în jos începând cu linia , iar coloanele sunt numerotate de la stânga la dreapta începând cu . În fiecare dintre câmpurile acestei table se scrie câte un număr natural din mulţimea după următoarele reguli:
- se porneşte din colţul aflat în poziţia stânga sus al tablei şi se avansează utilizând săritura calului
- se merge orizontal către dreapta şi în continuare, pe chenarul format din primele două linii, primele două coloane, ultimele două linii şi ultimele două coloane, în sensul acelor de ceasornic;
- se efectuează mai multe tururi ale tablei, până ce se umple întregul chenar, fără să se sară de două ori în aceeaşi căsuţă, fără să se sară în afara acestui chenar şi fără să rămână vreun câmp liber;
- din poziţia finală în care s-a ajuns, trebuie să fie posibilă săritura în colţul din stânga sus al pătratului rămas neacoperit;
- se continuă deplasarea în interiorul pătratului rămas neacoperit, folosind regulile a), b), c), d) până ce se ajunge la pătratul interior de latură care va conţine valoarea .
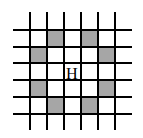
Amintim că o săritură a calului constă într-o deplasare de două căsuţe pe orizontală urmată de o deplasare de o căsuţă pe verticală sau într-o deplasare de două căsuţe pe verticală urmată de o deplasare de o căsuţă pe orizontală. Calul din figura următoare poate ajunge printr-o săritură în oricare dintre cele 8 poziţii haşurate:
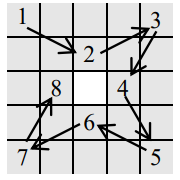
De exemplu, pentru , după un tur al tablei, se obţine următoarea acoperire parţială:
Iar după al doilea tur, se obţine acoperirea parţială:
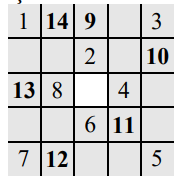
Pentru , acoperirea se realizează astfel:
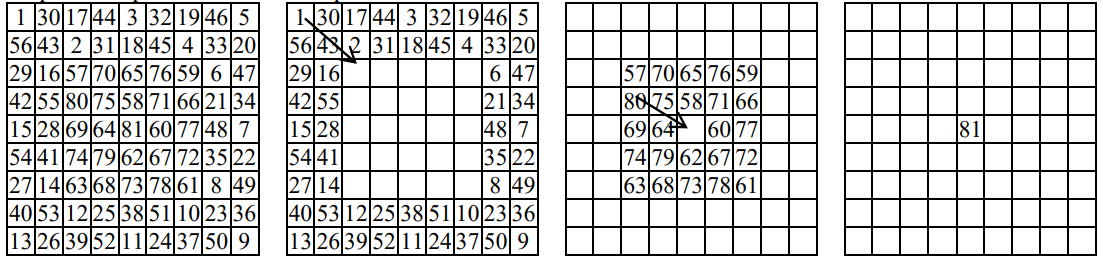
Cerinţă
Cunoscând valoarea lui ce reprezintă dimensiunea tablei şi un număr , să se determine linia şi coloana căsuţei din tabelă unde este scris numărul , după regulile de mai sus.
Date de intrare
Fişierul horse.in conţine două numere:
- numărul liniilor şi coloanelor tablei, pe prima linie
- numărul dintr-o căsuţă a tablei, pe a doua linie
Date de ieșire
Fişierul horse.out va conţine două numere: linia şi respectiv coloana căsuţei unde este scris numărul , cu un spaţiu între ele.
Restricții și precizări
- pentru dintre teste
Exemplul 1
horse.in
5
24
horse.out
2 1
Explicație
Pe o tablă numărul va ajunge pe linia şi coloana
Exemplul 2
horse.in
9
36
horse.out
8 9
Explicație
Pe o tablă numărul va ajunge pe linia şi coloana
Exemplul 3
horse.in
41
1000
horse.out
14 7
Explicație
Pe o tablă numărul va ajunge pe linia şi coloana